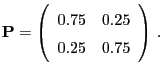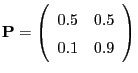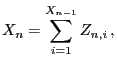(see. O. Häggström (2002) Finite Markov Chains and Algorithmic Applications. CU Press, Cambridge)
- We assume to observe the weather in an area whose typical weather is
characterized by longer periods of rainy or dry days (denoted by
rain and sunshine), where rain and sunshine exhibit approximately
the same relative frequency over the entire year.
- It is sometimes claimed that the best way to predict tomorrow's weather is simply to guess that it will be the same tomorrow as it is today.
- If we assume that this way of predicting the weather will be correct in 75% of the cases (regardless whether today's weather is rain or sunshine), then the weather can be easily modelled by a Markov chain.
- The state space consists of the two states
 rain and
rain and 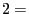 sunshine.
sunshine.
- The transition matrix is given as follows:
- Note that a crucial assumption for this model is the perfect
symmetry between rain and sunshine in the sense that the probability
that today's weather will persist tomorrow is the same regardless of
today's weather.
- In areas where sunshine is much more common than rain a more
realistic transition matrix would be the following:
- Classic examples for Markov chains are so-called random
walks. The (unbounded) basic model is defined in the following
way:
- Let
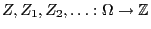 be a sequence of independent
and identically distributed random variables mapping to
be a sequence of independent
and identically distributed random variables mapping to
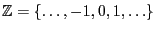 .
.
- Let
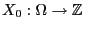 be an arbitrary random variable, which is
independent from the increments
be an arbitrary random variable, which is
independent from the increments
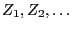 , and define
, and define
- Then the random variables
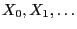 form a Markov chain on
the countably infinite state space
form a Markov chain on
the countably infinite state space
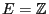 with initial distribution
with initial distribution
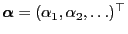 , where
, where
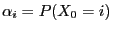 . The transition probabilities are given by
. The transition probabilities are given by
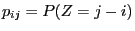 .
.
- Let
- Remarks
- The Markov chain given in (9) can be used as a
model for the temporal dynamics of the solvability reserve of
insurance companies.
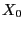 will then be interpreted as the
(random) initial reserve and the increments
will then be interpreted as the
(random) initial reserve and the increments 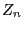 as the
difference
as the
difference
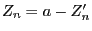 between the risk-free premium
income
between the risk-free premium
income 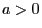 and random expenses for the liabilities
and random expenses for the liabilities
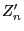 in time period
in time period 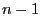 .
.
- Another example for a random walk are the total winnings in
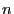 roulette games already discussed in Section WR-1.3. In this case
we have
roulette games already discussed in Section WR-1.3. In this case
we have 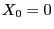 . The distribution of the random increment
. The distribution of the random increment 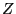 is
given by
is
given by
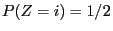 for
for 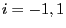 and
and 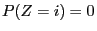 for
for
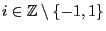 .
.
- The Markov chain given in (9) can be used as a
model for the temporal dynamics of the solvability reserve of
insurance companies.
- The number of customers waiting in front of an arbitrary but fixed
checkout desk in a grocery store can be modelled by a Markov chain
in the following way:
- Let
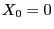 be the number of customers waiting in the line, when the
store opens.
be the number of customers waiting in the line, when the
store opens.
- By
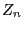 we denote the random number of new customers arriving
while the cashier is serving the
we denote the random number of new customers arriving
while the cashier is serving the 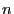 th customer (
th customer (
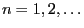 ).
).
- We assume the random variables
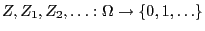 to be independent and
identically distributed.
to be independent and
identically distributed.
- Let
- The recursive definition
yields a sequence of random variables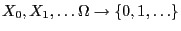 that is a Markov chain whose
transition matrix
that is a Markov chain whose
transition matrix
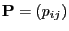 has the entries
has the entries
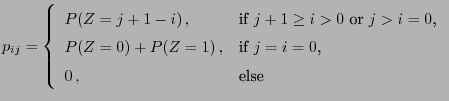
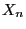 denotes the random number of customers waiting in the line
right after the cashier has finished serving the
denotes the random number of customers waiting in the line
right after the cashier has finished serving the 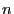 th customer,
i.e., the customer who has just started checking out and hence
already left the line is not counted any more.
th customer,
i.e., the customer who has just started checking out and hence
already left the line is not counted any more.
- We consider the reproduction process of a certain population,
where
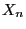 denotes the total number of descendants in the
denotes the total number of descendants in the 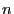 th
generation;
th
generation; 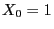 .
.
- We assume that
where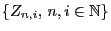 is a set of independent and
identically distributed random variables mapping into the set
is a set of independent and
identically distributed random variables mapping into the set
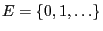 .
.
- The random variable
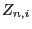 is the random number of descendants of
individual
is the random number of descendants of
individual 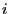 in generation
in generation 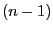 .
.
- The sequence
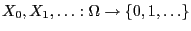 of random
variables given by
of random
variables given by 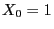 and the recursion (11)
is called a branching process.
and the recursion (11)
is called a branching process.
- One can show (see Section 2.1.3) that
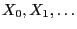 is a Markov chain with transition probabilities
is a Markov chain with transition probabilities
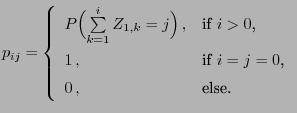
- Further examples of Markov chains can be constructed as follows (see
E. Behrends (2000) Introduction to Markov Chains. Vieweg,
Braunschweig, p.4).
- We consider the finite state space
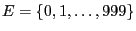 , the
initial distribution
, the
initial distribution
and the transition probabilities![$\displaystyle p_{ij}=\left\{\begin{array}{ll} \displaystyle\frac{1}{6}\;, &
\mb...
...mod(1000)\in\{1,\ldots,6\}$,}\\ [3\jot]
0\,, &\mbox{else.}
\end{array}\right.
$](img115.png)
- Let
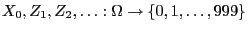 be
independent random variables, where the distribution of
be
independent random variables, where the distribution of 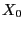 is
given by (12) and
is
given by (12) and
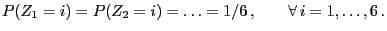
- The sequence
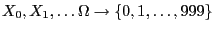 of random
variables defined by the recursion formula
of random
variables defined by the recursion formula
for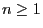 is a Markov chain called cyclic
random walk.
is a Markov chain called cyclic
random walk.
- We consider the finite state space
- Remarks
- An experiment corresponding to the Markov chain defined above can
be designed in the following way. First of all we toss a coin four
times and record the frequency of the event ``versus''. The
number
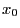 of these events is regarded as realization of the
random initial state
of these events is regarded as realization of the
random initial state 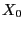 ; see the Bernoulli scheme in
Section WR-3.2.1.
; see the Bernoulli scheme in
Section WR-3.2.1.
- Afterwards a dice is tossed
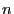 times. Die outcome
times. Die outcome 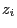 of the
of the
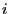 th experiment, is interpreted as a realization of the random
``increment''
th experiment, is interpreted as a realization of the random
``increment'' 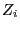 ;
;
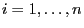 .
.
- The new state
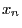 of the system results from the update of the old
state
of the system results from the update of the old
state 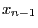 according to (13) taking
according to (13) taking 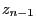 as increment.
as increment.
- If the experiment is not realized by tossing a coin and a dice,
respectively, but by a computer-based generation of pseudo-random numbers
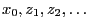 the procedure is
referred to as Monte-Carlo simulation.
the procedure is
referred to as Monte-Carlo simulation.
- Methods allowing the construction of dynamic simulation algorithms based on Markov chains will be discussed in the second part of this course in detail; see Chapter 3 below.
- An experiment corresponding to the Markov chain defined above can
be designed in the following way. First of all we toss a coin four
times and record the frequency of the event ``versus''. The
number