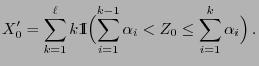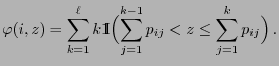Next: The Matrix of the
Up: Specification of the Model
Previous: Examples
Contents
Recursive Representation
- In this section we will show
- how Markov chains can be constructed from sequences of independent
and identically distributed random variables,
- that the recursive formulaź (9),
(10), (11) and (13)
are special cases of a general principle for the construction of
Markov chains,
- that vice versa every Markov chain can be considered as solution of
a recursive stochastic equation.
- As usual let
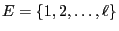 be a finite (or countably
infinite) set.
be a finite (or countably
infinite) set.
- Proof
-
- Remarks
-
Our next step will be to show that vice versa, every Markov chain
can be regarded as the solution of a recursive stochastic equation.
- Remarks
-
- If (16) holds for two sequences
 and
and
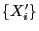 of random variables, these sequences
are called stochastically equivalent.
of random variables, these sequences
are called stochastically equivalent.
- The construction principle (17)-(19)
can be exploited for the Monte-Carlo simulation of Markov chains
with given initial distribution and transition matrix.
- Markov chains on a countably infinite state space can be
constructed and simulated in the same way. However, in this case
(17)-(19) need to be modified by
considering vectors
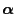 and matrices
and matrices
 of infinite
dimensions.
of infinite
dimensions.




Next: The Matrix of the
Up: Specification of the Model
Previous: Examples
Contents
Ursa Pantle
2006-07-20
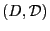 be a measurable space, e.g.
be a measurable space, e.g.
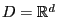 could be the
could be the 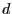 -dimensional Euclidian space and
-dimensional Euclidian space and
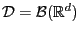 the Borel
the Borel 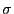 -algebra on
-algebra on
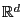 , or
, or
![$ D=[0,1]$](img135.png) could be defined as the unit interval and
could be defined as the unit interval and
![$ \mathcal{D}=\mathcal{B}([0,1])$](img136.png) as the Borel
as the Borel 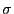 -algebra on
-algebra on ![$ [0,1]$](img137.png) .
.
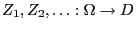 be a sequence of independent
and identically distributed random variables mapping into
be a sequence of independent
and identically distributed random variables mapping into 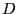 , and
let
, and
let
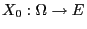 be independent of
be independent of
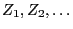 .
.
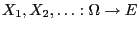 be given by
the stochastic recursion equation
be given by
the stochastic recursion equation
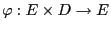 is an arbitrary measurable
function.
is an arbitrary measurable
function.
![$\displaystyle \qquad
Z_0\in\Bigl(\sum_{i=1}^{k-1}
\alpha_i,\sum_{i=1}^{k}\alpha_i\Bigr]\,,
$](img168.png)