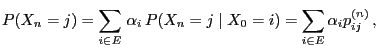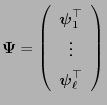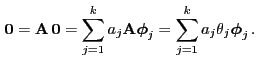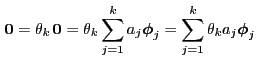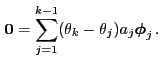Next: Ergodicity and Stationarity
Up: Specification of the Model
Previous: Recursive Representation
Contents
The Matrix of the  -Step Transition Probabilities
-Step Transition Probabilities
- Remarks
-
- The matrix
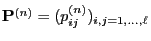 is
called the
is
called the  -step transition matrix of the Markov chain
-step transition matrix of the Markov chain
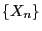 .
.
- If we introduce the convention
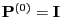 , where
, where
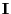 denotes the
denotes the
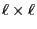 -dimensional identity matrix, then
-dimensional identity matrix, then
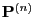 has the following representation formulae.
has the following representation formulae.
Lemma 2.1
The equation
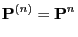 |
(22) |
holds for arbitrary
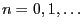
and thus for arbitrary
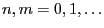
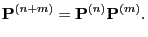 |
(23) |
- Proof
 Equation (22) is an immediate consequence of
(20) and the definition of matrix multiplication.
Equation (22) is an immediate consequence of
(20) and the definition of matrix multiplication.

- Example
 (Weather Forecast)
(Weather Forecast)
- Consider
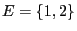 , and let
be an arbitrarily chosen transition matrix, i.e.
, and let
be an arbitrarily chosen transition matrix, i.e.
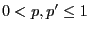 .
.
- One can show that the
 -step transition matrix
-step transition matrix
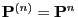 is given by the formula
is given by the formula
- Remarks
-
- The matrix identity (23) is called the Chapman-Kolmogorov equation in literature.
- Formula (23) yields the following useful
inequalities.
Furthermore, Lemma 2.1 allows the following
representation of the distribution of 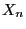 . Recall that
. Recall that 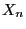 denotes the state of the Markov chain at step
denotes the state of the Markov chain at step  .
.
- Proof
-
- From the formula of total probability (see Theorem WR-2.6) and
(21) we conclude that
where we define
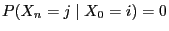 if
if
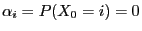 .
.
- Now statement (26) follows from Lemma 2.1.

- Remarks
-
- Due to Theorem 2.3 the probabilities
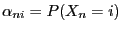 can be calculated via the
can be calculated via the  th power
th power
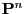 of the transition matrix
of the transition matrix
 .
.
- In this context it is often useful to find a so-called spectral representation of
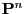 . It can be constructed by
using the eigenvalues and a basis of eigenvectors of the
transition matrix as follows. Note that there are matrices having
no spectral representation.
. It can be constructed by
using the eigenvalues and a basis of eigenvectors of the
transition matrix as follows. Note that there are matrices having
no spectral representation.
- A short recapitulation
- If the eigenvectors are
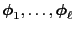 linearly
independent,
linearly
independent,
- the inverse
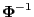 exists and we can set
exists and we can set
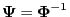 .
.
- Moreover, in this case (29) implies
and hence
- This yields the spectral representation of
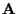 :
:
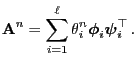 |
(30) |
- Remarks
-
- Proof
-
- The first statement will be proved by complete induction.
- If the eigenvalues
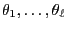 of
of
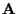 are
pairwise distinct,
are
pairwise distinct,
- the
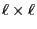 matrix
matrix
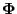 consists of
consists of 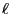 linearly
independent column vectors,
linearly
independent column vectors,
- and thus
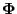 is invertible.
is invertible.
- Consequently, the matrix
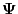 of the left eigenvectors is
simply the inverse
of the left eigenvectors is
simply the inverse
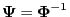 . This immediately implies
(31).
. This immediately implies
(31).





Next: Ergodicity and Stationarity
Up: Specification of the Model
Previous: Recursive Representation
Contents
Ursa Pantle
2006-07-20
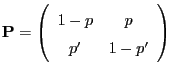
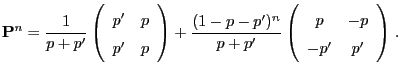
![]() . Recall that
. Recall that ![]() denotes the state of the Markov chain at step
denotes the state of the Markov chain at step ![]() .
.