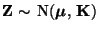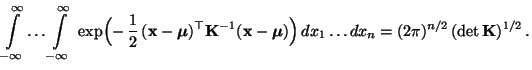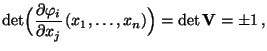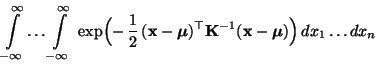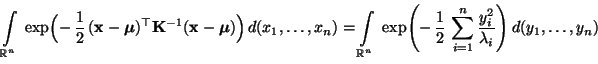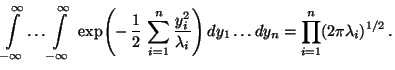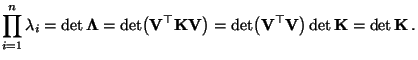Next: Charakteristiken der multivariaten Normalverteilung
Up: Multivariate Normalverteilung
Previous: Multivariate Normalverteilung
Contents
Definition und grundlegende Eigenschaften
- Beachte
-
- Jede symmetrische und positiv definite Matrix
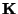 ist regulär,
d.h., die inverse Matrix
ist regulär,
d.h., die inverse Matrix
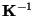 ist wohldefiniert. (Wegen
Theorem 3.1 ist die gleichbedeutend damit, daß
ist wohldefiniert. (Wegen
Theorem 3.1 ist die gleichbedeutend damit, daß
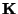 vollen Rang hat bzw.
vollen Rang hat bzw.
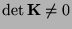 .)
.)
- Dies ergibt sich aus der folgenden Überlegung: Falls
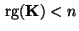 gilt, d.h., falls es einen Vektor
gilt, d.h., falls es einen Vektor
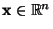 mit
mit
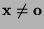 gibt, so daß
gibt, so daß
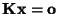 , dann gilt
auch
, dann gilt
auch
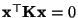 , d.h.,
, d.h.,
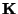 ist nicht positiv
definit.
ist nicht positiv
definit.
Um zu zeigen, daß die in (33) gegebene Funktion
eine Wahrscheinlichkeitsdichte ist, sind die folgenden Begriffe
und Aussagen der Matrix-Algebra nützlich.
- Definition
 Sei
Sei
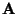 eine beliebige
eine beliebige
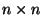 Matrix. Jede (komplexe) Zahl
Matrix. Jede (komplexe) Zahl
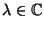 , für die
es einen Vektor
, für die
es einen Vektor
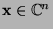 mit
mit
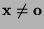 gibt, so daß
gibt, so daß
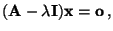 |
(34) |
heißt Eigenwert der Matrix
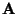 . Außerdem sagt man dann,
daß
. Außerdem sagt man dann,
daß
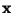 ein zu
ein zu 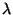 gehörender Eigenvektor ist.
gehörender Eigenvektor ist.
- Beachte
-
Lemma 3.8

Sei
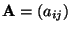
eine
symmetrische
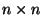
Matrix mit reellwertigen Einträgen
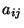
. Dann sind sämtliche Eigenwerte reell, und die zu
verschiedenen Eigenwerten
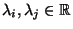
gehörenden
Eigenvektoren
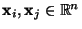
sind zueinander
orthogonal.
- Beweis
-
- Weil die Elemente von
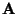 reelle Zahlen sind, ist für jede
Lösung
reelle Zahlen sind, ist für jede
Lösung
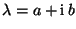 von (35) gleichzeitig
auch
von (35) gleichzeitig
auch
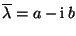 eine Lösung von
(35).
eine Lösung von
(35).
- Seien
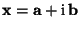 und
und
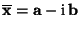 Eigenvektoren, die zu
Eigenvektoren, die zu 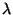 bzw.
bzw.
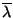 gehören.
Dann gilt
gehören.
Dann gilt
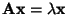 und
und
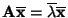 bzw.
und
bzw.
und
- Hieraus folgt, daß
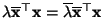 .
.
- Weil
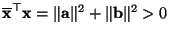 , ergibt
sich hieraus, daß
, ergibt
sich hieraus, daß
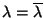 , d.h.,
, d.h., 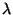 ist
eine reelle Zahl.
ist
eine reelle Zahl.
- Auf ähnliche Weise läßt sich zeigen, daß es zu verschiedenen
Eigenwerten
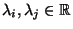 gehörende Eigenvektoren
gehörende Eigenvektoren
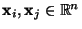 mit reellwertigen Komponenten gibt, die
zueinander orthogonal sind.
mit reellwertigen Komponenten gibt, die
zueinander orthogonal sind.
- Weil die Matrix
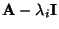 nur reellwertige
Eintragungen hat, sind mit
nur reellwertige
Eintragungen hat, sind mit
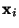 auch
auch
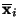 bzw.
bzw.
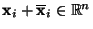 zu
zu 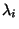 gehörende
Eigenvektoren.
gehörende
Eigenvektoren.
- Wir können (und werden) deshalb o.B.d.A. annehmen, daß
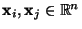 . Aus der Gültigkeit von
. Aus der Gültigkeit von
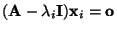
und
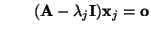
ergibt sich außerdem, daß
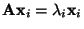
und
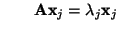
bzw.
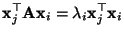
und
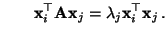
- Andererseits gilt offenbar
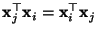 , und aus der Symmetrie
von
, und aus der Symmetrie
von
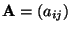 ergibt sich die Identität
ergibt sich die Identität
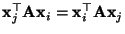 , denn es gilt
, denn es gilt
- Insgesamt ergibt sich somit, daß
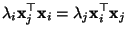
bzw.
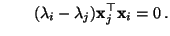
- Wegen
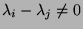 folgt hieraus, daß
folgt hieraus, daß
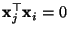 .
.

- Beachte
-
- Beweis
-
Wir zeigen nun, daß die in (33) gegebene Funktion
eine (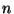 -dimensionale) Wahrscheinlichkeitsdichte ist.
-dimensionale) Wahrscheinlichkeitsdichte ist.
Theorem 3.7

Sei
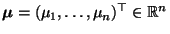
ein beliebiger
Vektor, und sei
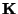
eine symmetrische und positiv definite
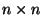
-Matrix. Dann gilt
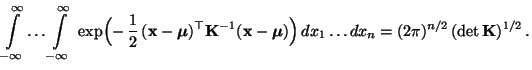 |
(39) |
- Beweis
-
- Weil
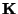 symmetrisch und positiv definit (und damit auch
regulär) ist, gibt es wegen Lemma 3.9 eine
symmetrisch und positiv definit (und damit auch
regulär) ist, gibt es wegen Lemma 3.9 eine 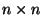 Matrix
Matrix
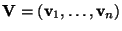 , die aus den
orthonormalen Eigenvektoren
, die aus den
orthonormalen Eigenvektoren
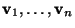 von
von
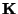 besteht, so daß
besteht, so daß
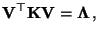 |
(40) |
wobei
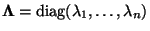 die
die
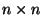 Diagonalmatrix bezeichnet, die aus den Eigenwerten
Diagonalmatrix bezeichnet, die aus den Eigenwerten
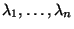 von
von
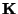 gebildet wird.
gebildet wird.
- Außerdem ergibt sich aus der positiven Definitheit von
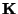 ,
daß
,
daß
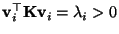 für jedes
für jedes
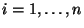 , d.h., sämtliche Eigenwerte
, d.h., sämtliche Eigenwerte
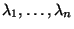 von
von
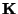 sind positiv.
sind positiv.
- Wegen
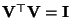 gilt auch
gilt auch
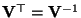 bzw.
bzw.
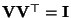 .
.
- Weil außerdem
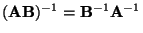 gilt,
ergibt sich hieraus und aus (40), daß
gilt,
ergibt sich hieraus und aus (40), daß
- Die Abbildung
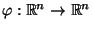 mit
mit
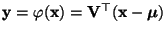 , d.h.
, d.h.
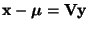 , bildet den
, bildet den
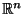 auf sich selbst ab,
und für die Jacobi-Determinante der Abbildung
auf sich selbst ab,
und für die Jacobi-Determinante der Abbildung
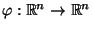 gilt
wobei sich die letzte Gleichheit aus der Tatsache ergibt, daß
gilt
wobei sich die letzte Gleichheit aus der Tatsache ergibt, daß
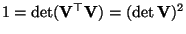 .
.
- Für das Integral auf der linken Seite von (39)
gilt somit, daß
- Hieraus ergibt sich die Behauptung, weil





Next: Charakteristiken der multivariaten Normalverteilung
Up: Multivariate Normalverteilung
Previous: Multivariate Normalverteilung
Contents
Ursa Pantle
2003-03-10
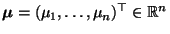 ein beliebiger
Vektor, und sei
ein beliebiger
Vektor, und sei
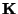 eine symmetrische und positiv definite
eine symmetrische und positiv definite
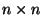 -Matrix, d.h., es gelte
-Matrix, d.h., es gelte
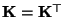 und
und
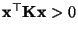 für jeden Vektor
für jeden Vektor
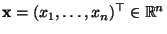 mit
mit
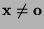 .
.
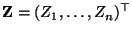 ein absolutstetiger
Zufallsvektor, wobei die gemeinsame Dichte von
ein absolutstetiger
Zufallsvektor, wobei die gemeinsame Dichte von
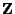 gegeben sei
durch
gegeben sei
durch
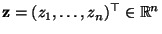 .
.
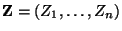 (multivariat) normalverteilt ist.
(multivariat) normalverteilt ist.