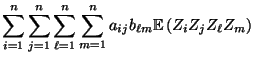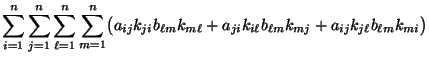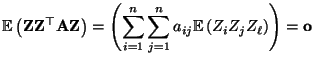- Seien
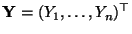 und
und
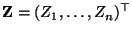 beliebige
beliebige 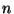 -dimensionale
Zufallsvektoren, und sei
-dimensionale
Zufallsvektoren, und sei
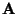 eine symmetrische
eine symmetrische 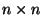 Matrix mit reellwertigen Eintragungen.
Matrix mit reellwertigen Eintragungen.
- Dann heißt die (reellwertige) Zufallsvariable
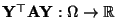 quadratische Form von
quadratische Form von
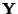 bezüglich
bezüglich
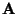 .
.
- Die Zufallsvariable
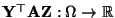 heißt bilineare Form von
heißt bilineare Form von
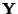 und
und
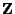 bezüglich
bezüglich
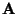 .
.