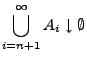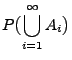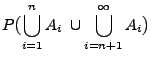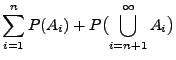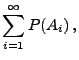Next: Endliche Wahrscheinlichkeitsräume
Up: Wahrscheinlichkeitsmaße
Previous: Definition und elementare Eigenschaften
Contents
Weitere Eigenschaften von
Wahrscheinlichkeitsmaßen
Die Subadditivität von Wahrscheinlichkeitsmaßen, die in
Teilaussage 4 von Theorem 2.1 betrachtet wurde, gilt
nicht nur für zwei bzw. endlich viele Ereignisse, sondern auch für
Folgen von unendlich vielen Ereignissen.
Theorem 2.2
Sei
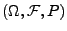
ein
Wahrscheinlichkeitsraum, und
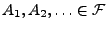
seien beliebige Ereignisse. Dann gilt
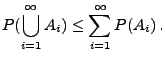 |
(7) |
Beweis Anstelle der Folge
Anstelle der Folge 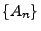 betrachten wir die
Folge
betrachten wir die
Folge
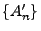 von paarweise disjunkten Mengen, wobei
Dann gilt
wobei sich die letzte
Ungleichung aus der Monotonie von Wahrscheinlichkeitsmaßen ergibt.
von paarweise disjunkten Mengen, wobei
Dann gilt
wobei sich die letzte
Ungleichung aus der Monotonie von Wahrscheinlichkeitsmaßen ergibt.

Das folgende Korollar wird in der Literatur das Lemma von
Borel-Cantelli genannt.
Korollar 2.3
Sei
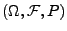
ein
Wahrscheinlichkeitsraum und
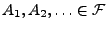
eine beliebige Folge von Ereignissen. Dann gilt
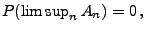 |
(8) |
falls
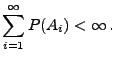 |
(9) |
Beweis Aus Korollar 2.2 und
Theorem 2.2 ergibt sich, dass
Aus Korollar 2.2 und
Theorem 2.2 ergibt sich, dass
wobei sich die letzte Gleichheit aus der
Summierbarkeitsbedingung (9) ergibt.

Wir diskutieren nun den Zusammenhang zwischen der
 -Additivität und gewissen Stetigkeitseigenschaften von
Mengenfunktionen.
-Additivität und gewissen Stetigkeitseigenschaften von
Mengenfunktionen.
- Beweis
 Wir führen einen zyklischen Beweis, d.h., wir zeigen,
dass die folgenden Implikationen richtig sind:
Wir führen einen zyklischen Beweis, d.h., wir zeigen,
dass die folgenden Implikationen richtig sind:
- 1.
 2.
2.
-
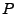 sei
sei 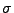 -additiv, und
es gelte
-additiv, und
es gelte
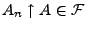 . Die Behauptung ergibt sich dann
genauso wie im Beweis von Korollar 2.2.
. Die Behauptung ergibt sich dann
genauso wie im Beweis von Korollar 2.2.
- 2.
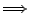 3.
3.
-
Es gelte
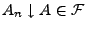 . Hieraus folgt, dass
. Hieraus folgt, dass
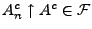 . Also ergibt sich aus Aussage 2, dass
. Also ergibt sich aus Aussage 2, dass
- 3.
 4.
4.
-
Diese Implikation gilt offensichtlich, weil die Teilaussage 4 ein
Spezialfall von Teilaussage 3 ist.
- 4.
 1.
1.
-
Seien
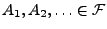 paarweise disjunkte Mengen. Dann
gilt
Also ist
paarweise disjunkte Mengen. Dann
gilt
Also ist
wobei sich
die zweite Gleichheit aus der endlichen Additivität von 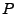 ergibt.
ergibt.

Für Wahrscheinlichkeitsmaße, d.h. für 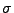 -additive
Mengenfunktionen lassen sich die in Theorem 2.3
betrachteten drei Stetigkeitseigenschaften wie folgt zu einer Stetigkeitseigenschaft zusammenfassen.
-additive
Mengenfunktionen lassen sich die in Theorem 2.3
betrachteten drei Stetigkeitseigenschaften wie folgt zu einer Stetigkeitseigenschaft zusammenfassen.
Theorem 2.4
Sei
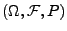
ein
Wahrscheinlichkeitsraum, und
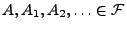
seien beliebige Ereignisse. Dann gilt
 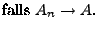 |
(10) |
Beweis Die Behauptung folgt unmittelbar aus dem Ergebnis
von Übungsaufgabe 2.1, denn in dieser Übungsaufgabe wird gezeigt,
dass
und
Weil
Die Behauptung folgt unmittelbar aus dem Ergebnis
von Übungsaufgabe 2.1, denn in dieser Übungsaufgabe wird gezeigt,
dass
und
Weil
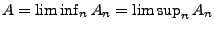 , ergibt sich hieraus, dass
und damit, dass
, ergibt sich hieraus, dass
und damit, dass
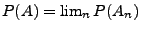 .
.





Next: Endliche Wahrscheinlichkeitsräume
Up: Wahrscheinlichkeitsmaße
Previous: Definition und elementare Eigenschaften
Contents
Ursa Pantle
2004-05-10
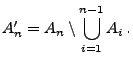
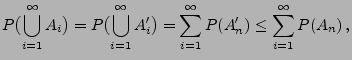
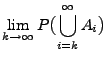
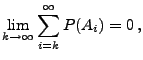
![]() -Additivität und gewissen Stetigkeitseigenschaften von
Mengenfunktionen.
-Additivität und gewissen Stetigkeitseigenschaften von
Mengenfunktionen.
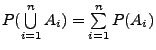 gelte für jede endliche Folge von paarweise disjunkten Mengen
gelte für jede endliche Folge von paarweise disjunkten Mengen