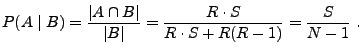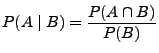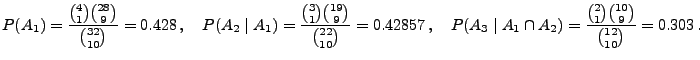Next: Formel der totalen Wahrscheinlichkeit;
Up: Bedingte Wahrscheinlichkeiten
Previous: Bedingte Wahrscheinlichkeiten
Contents
Definition und Multiplikationssatz
Häufig verfügen wir bei der Durchführung von Experimenten über
Vorinformationen, die bei der Berechnung von Wahrscheinlichkeiten
interessierender Ereignisse berücksichtigt werden sollen.
Bei manchen Untersuchungen wird jedoch lediglich (hypothetisch)
angenommen, dass eine bestimmte Vorinformation vorliegt, wobei
dann unter dieser hypothetischen Annahme gerechnet wird. Diese
sogenannte Bayessche Methodik wird im weiteren Verlauf der
Vorlesung noch genauer diskutiert.
- Beispiele
-
- Skatspiel
- Die Kenntnis der eigenen 10 Karten soll als Vorinformation über
die Verteilung der übrigen 22 Karten genutzt werden.
- Markieren die 32 Karten mit den Zahlen
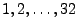 .
.
- Betrachten Laplaceschen Wahrscheinlichkeitsraum,
wobei
 die Menge aller Permutationen von
die Menge aller Permutationen von 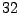 Elementen ist
(
Elementen ist
(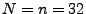 ; mit Reihenfolge und ohne Zurücklegen)
; mit Reihenfolge und ohne Zurücklegen)
- Gesucht sei die Wahrscheinlichkeit des Ereignisses
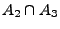 , wobei
, wobei 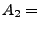 {Spieler 2 hat
{Spieler 2 hat 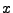 Asse},
Asse}, 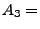 {Spieler 3 hat
{Spieler 3 hat 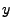 Asse}, unter der Bedingung, dass das Ereignis
Asse}, unter der Bedingung, dass das Ereignis 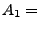 {Spieler
1 hat die Karten mit den Nummern
{Spieler
1 hat die Karten mit den Nummern
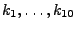 }
eintritt.
}
eintritt.
- Lösungsansatz: Beziehen die Anzahl der
Permutationen, bei denen
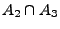 eintritt, nicht auf die
Gesamtanzahl
eintritt, nicht auf die
Gesamtanzahl 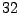 ! aller möglichen Permutationen, sondern
lediglich auf diejenigen Permutationen, bei denen das Ereignis
! aller möglichen Permutationen, sondern
lediglich auf diejenigen Permutationen, bei denen das Ereignis
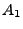 eintritt.
eintritt.
- D.h., die gesuchte Wahrscheinlichkeit ist die
(bedingte) relative Häufigkeit
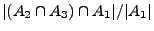
- Dabei benutzen wir die Schreibweise:
und nennen diese Größe bedingte Wahrscheinlichkeit des
Ereignisses
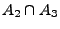 unter der Bedingung, dass das
Ereignis
unter der Bedingung, dass das
Ereignis 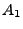 eintritt.
eintritt.
- Urnenmodell
- Betrachten Urne mit
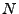 Elementen (
Elementen (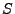 schwarze,
schwarze, 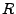 rote
Kugeln), d.h.
rote
Kugeln), d.h. 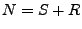 , vgl. Abschnitt 3.2.2;
, vgl. Abschnitt 3.2.2;
- 2 Elemente,
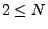 , sollen insgesamt ausgewählt werden
(ohne Zurücklegen);
, sollen insgesamt ausgewählt werden
(ohne Zurücklegen);
- Sei
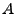 das Ereignis, beim zweiten Versuch ,,schwarz'' zu
ziehen, und sei
das Ereignis, beim zweiten Versuch ,,schwarz'' zu
ziehen, und sei 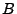 das Ereignis, beim ersten Versuch
,,rot'' zu ziehen.
das Ereignis, beim ersten Versuch
,,rot'' zu ziehen.
- Gesucht ist die bedingte
Wahrscheinlichkeit
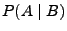 , beim zweiten Versuch ,,schwarz'' zu
ziehen, falls beim ersten Versuch ,,rot'' gezogen wird.
, beim zweiten Versuch ,,schwarz'' zu
ziehen, falls beim ersten Versuch ,,rot'' gezogen wird.
- Es gilt
Dies führt zu der folgenden (allgemeineren) Begriffsbildung.
- Definition
 Seien
Seien
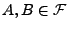 seien beliebige Ereignisse mit
seien beliebige Ereignisse mit 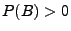 . Dann heißt
. Dann heißt
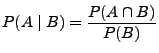 |
(13) |
die bedingte Wahrscheinlichkeit von 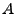 unter der Bedingung
unter der Bedingung
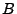 .
.
- Beachte
 Die Definitionsgleichung (13)
kann in der Form
Die Definitionsgleichung (13)
kann in der Form
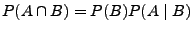 geschrieben
werden. Durch Iteration dieser Überlegung ergibt sich der
folgende Multiplikationssatz.
geschrieben
werden. Durch Iteration dieser Überlegung ergibt sich der
folgende Multiplikationssatz.
- Beweis
- klar
- Beispiel
- (Skatspiel)
- Betrachten das Ereignis
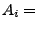 {Spieler
{Spieler 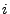 erhält genau ein As};
erhält genau ein As}; 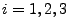 .
.
- Gesucht ist die Wahrscheinlichkeit
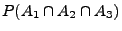 ,
dass jeder der drei Spieler genau ein As erhält?
,
dass jeder der drei Spieler genau ein As erhält?
- Lösung: Es gilt
- Hieraus und aus (14) ergibt sich




Next: Formel der totalen Wahrscheinlichkeit;
Up: Bedingte Wahrscheinlichkeiten
Previous: Bedingte Wahrscheinlichkeiten
Contents
Ursa Pantle
2004-05-10
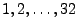 .
.
 die Menge aller Permutationen von
die Menge aller Permutationen von 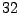 Elementen ist
(
Elementen ist
(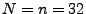 ; mit Reihenfolge und ohne Zurücklegen)
; mit Reihenfolge und ohne Zurücklegen)
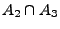 , wobei
, wobei 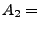 {Spieler 2 hat
{Spieler 2 hat 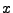 Asse},
Asse}, 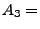 {Spieler 3 hat
{Spieler 3 hat 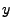 Asse}, unter der Bedingung, dass das Ereignis
Asse}, unter der Bedingung, dass das Ereignis 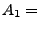 {Spieler
1 hat die Karten mit den Nummern
{Spieler
1 hat die Karten mit den Nummern
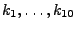 }
eintritt.
}
eintritt.
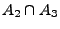 eintritt, nicht auf die
Gesamtanzahl
eintritt, nicht auf die
Gesamtanzahl 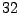 ! aller möglichen Permutationen, sondern
lediglich auf diejenigen Permutationen, bei denen das Ereignis
! aller möglichen Permutationen, sondern
lediglich auf diejenigen Permutationen, bei denen das Ereignis
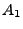 eintritt.
eintritt.
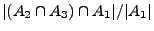
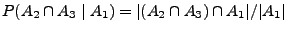
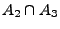 unter der Bedingung, dass das
Ereignis
unter der Bedingung, dass das
Ereignis 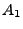 eintritt.
eintritt.
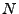 Elementen (
Elementen (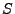 schwarze,
schwarze, 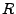 rote
Kugeln), d.h.
rote
Kugeln), d.h. 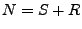 , vgl. Abschnitt 3.2.2;
, vgl. Abschnitt 3.2.2;
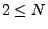 , sollen insgesamt ausgewählt werden
(ohne Zurücklegen);
, sollen insgesamt ausgewählt werden
(ohne Zurücklegen);
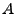 das Ereignis, beim zweiten Versuch ,,schwarz'' zu
ziehen, und sei
das Ereignis, beim zweiten Versuch ,,schwarz'' zu
ziehen, und sei 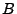 das Ereignis, beim ersten Versuch
,,rot'' zu ziehen.
das Ereignis, beim ersten Versuch
,,rot'' zu ziehen.
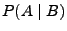 , beim zweiten Versuch ,,schwarz'' zu
ziehen, falls beim ersten Versuch ,,rot'' gezogen wird.
, beim zweiten Versuch ,,schwarz'' zu
ziehen, falls beim ersten Versuch ,,rot'' gezogen wird.