



Next: Verteilung und Verteilungsfunktion
Up: Zufallsvariablen und Zufallsvektoren
Previous: Zufallsvariablen und Zufallsvektoren
Contents
Definition von Zufallsvariablen
Betrachten einen beliebigen Wahrscheinlichkeitsraum
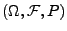 und ein beliebiges Element
und ein beliebiges Element
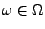 ,
wobei wir so wie bisher
,
wobei wir so wie bisher
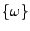 als Elementarereignis bzw.
Versuchsergebnis interpretieren.
als Elementarereignis bzw.
Versuchsergebnis interpretieren.
- Beachte
 Häufig interessiert nicht
Häufig interessiert nicht 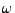 selbst, sondern
eine (quantitative oder qualitative)
Kennzahl
selbst, sondern
eine (quantitative oder qualitative)
Kennzahl 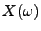 von
von 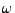 , d.h., wir betrachten die Abbildung
, d.h., wir betrachten die Abbildung
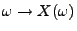 .
.
- Beispiele
-
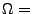 Menge von Eintragungen in einem Telefonbuch
Menge von Eintragungen in einem Telefonbuch
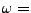 Familienname,
Familienname,
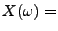 Anzahl der Buchstaben von
Anzahl der Buchstaben von 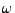
oder
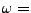 Telefonnummer,
Telefonnummer,
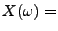 Anzahl der Ziffer ,,1'' in
Anzahl der Ziffer ,,1'' in 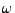
- zweimaliges Würfeln
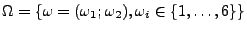
Augensumme
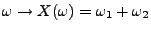
Sei
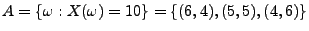 bzw. allgemeiner
bzw. allgemeiner
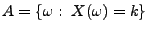 , wobei
, wobei
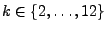 .
.
Gesucht ist die Wahrscheinlichkeit 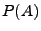 .
Hierfür ist es erforderlich, dass
.
Hierfür ist es erforderlich, dass
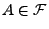 .
.
Allgemein muss also
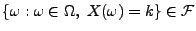 für jedes
für jedes
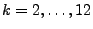 gelten.
gelten.
Bei diesem Beispiel ist das gleichbedeutend mit
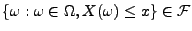 für jedes
für jedes
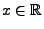 .
.
Das führt zu der folgenden Begriffsbildung.
- Definition
 Sei
Sei
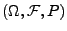 ein beliebiger
Wahrscheinlichkeitsraum.
Die Abbildung
ein beliebiger
Wahrscheinlichkeitsraum.
Die Abbildung
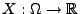 heißt Zufallsvariable
(bzw. Zufallsgröße), falls
heißt Zufallsvariable
(bzw. Zufallsgröße), falls
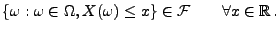 |
(1) |
- Beachte
-
- Die Regularitätsbedingung (1) wird Messbarkeit
der Abbildung
 bezüglich der
bezüglich der 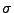 -Algebra
-Algebra
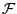 genannt.
genannt.
- In vielen Fällen interessiert nicht nur die
Wahrscheinlichkeit, dass die Werte
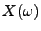 der Zufallsvariablen
der Zufallsvariablen  einen vorgegebenen Schwellenwert
einen vorgegebenen Schwellenwert 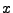 nicht
überschreiten, d.h., dass
nicht
überschreiten, d.h., dass  Werte im Intervall
Werte im Intervall
![$ B=(-\infty,x]$](img466.png) annimmt.
annimmt.
- Oftmals interessiert auch die Wahrscheinlichkeit, dass
 Werte in einer allgemeineren Teilmenge
Werte in einer allgemeineren Teilmenge
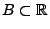 annimmt, wobei
annimmt, wobei 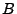 beispielsweise die Vereinigung von mehreren
disjunkten Intervallen sein kann.
beispielsweise die Vereinigung von mehreren
disjunkten Intervallen sein kann.
- Deshalb wird nicht nur im Grundraum
 , sondern
auch im Bildraum
, sondern
auch im Bildraum
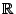 ein System
von Teilmengen von
ein System
von Teilmengen von
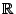 betrachtet, das abgeschlossen
bezüglich der Mengenoperationen
betrachtet, das abgeschlossen
bezüglich der Mengenoperationen
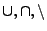 ist.
ist.
- Dabei wird oft die Borel-
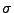 -Algebra
-Algebra
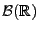 betrachtet,
die definiert ist als die kleinste
betrachtet,
die definiert ist als die kleinste 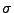 -Algebra
von Teilmengen von
-Algebra
von Teilmengen von
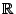 , die alle offenen Intervalle
, die alle offenen Intervalle
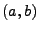 enthält;
enthält;
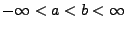 . D.h.
. D.h.
- Insbesondere enthält
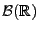 auch alle halboffenen bzw.
abgeschlossenen Intervalle, denn es gilt
auch alle halboffenen bzw.
abgeschlossenen Intervalle, denn es gilt
- Für jede abzählbare Teilmenge
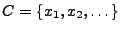 von
von
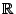 gilt
gilt
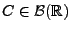 , denn für jedes
, denn für jedes
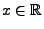 gilt
gilt
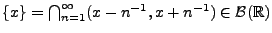 und
damit auch
und
damit auch
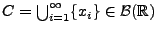 .
.




Next: Verteilung und Verteilungsfunktion
Up: Zufallsvariablen und Zufallsvektoren
Previous: Zufallsvariablen und Zufallsvektoren
Contents
Ursa Pantle
2004-05-10
 Menge von Eintragungen in einem Telefonbuch
Menge von Eintragungen in einem Telefonbuch
 Familienname,
Familienname,
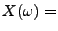 Anzahl der Buchstaben von
Anzahl der Buchstaben von 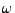
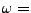 Telefonnummer,
Telefonnummer,
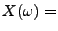 Anzahl der Ziffer ,,1'' in
Anzahl der Ziffer ,,1'' in 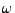
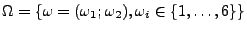
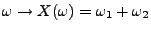
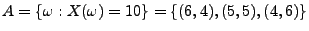 bzw. allgemeiner
bzw. allgemeiner
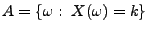 , wobei
, wobei
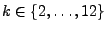 .
.
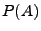 .
Hierfür ist es erforderlich, dass
.
Hierfür ist es erforderlich, dass
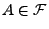 .
.
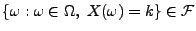 für jedes
für jedes
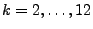 gelten.
gelten.
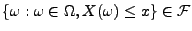 für jedes
für jedes
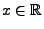 .
.
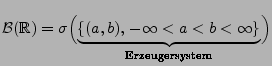
![$\displaystyle (a,b]=\bigcap_{n=1}^\infty(a,b+n^{-1})\in\mathcal{B}(\mathbb{R}),...
...,\quad
[a,b]=\bigcap_{n=1}^\infty(a-n^{-1},b+n^{-1})\in\mathcal{B}(\mathbb{R}).$](img473.png)