



Next: Unabhängige Zufallsvariablen
Up: Zufallsvektoren
Previous: Weitere Beispiele von Zufallsvektoren
Contents
Bedingte Wahrscheinlichkeitsfunktion; bedingte Verteilung;
bedingte Dichte
Analog zu dem in Abschnitt 2.6.1 eingeführten Begriff
der bedingten Wahrscheinlichkeit definieren wir nun die Begriffe
der bedingten Verteilung bzw. der bedingten Dichte.
- Definition
 (bedingte Wahrscheinlichkeitsfunktion und bedingte Verteilung)
(bedingte Wahrscheinlichkeitsfunktion und bedingte Verteilung)
- Sei
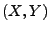 ein diskreter Zufallsvektor mit
ein diskreter Zufallsvektor mit
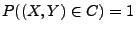 für
eine abzählbare Menge
für
eine abzählbare Menge
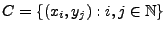 .
.
- Für jedes
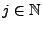 mit
mit
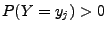 heißt dann
heißt dann
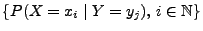 die bedingte
Wahrscheinlichkeitsfunktion von
die bedingte
Wahrscheinlichkeitsfunktion von  unter der Bedingung
unter der Bedingung
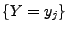 .
.
- Sie bestimmt die bedingte
Verteilung
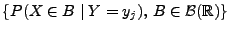 von
von  unter der Bedingung
unter der Bedingung 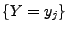 eindeutig.
eindeutig.
- Analog heißt
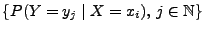 bzw.
bzw.
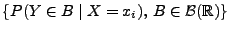 für jedes
für jedes
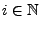 mit
mit
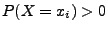 die bedingte Wahrscheinlichkeitsfunktion bzw. bedingte Verteilung
von
die bedingte Wahrscheinlichkeitsfunktion bzw. bedingte Verteilung
von 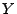 unter der Bedingung
unter der Bedingung  .
.
- Definition
 (bedingte Dichte)
(bedingte Dichte)
- Beispiele
-
- zweimaliges Würfeln
Sei
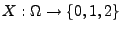 bzw.
bzw.
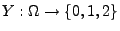 die (zufällige) Anzahl, mit der die Augenzahl ,,6'' bzw. ,,1''
beim zweimaligen Würfeln erzielt wird; vgl.
Abschnitt 3.3.1. Dann ergeben sich die folgenden bedingten
Wahrscheinichkeitsfunktionen von
die (zufällige) Anzahl, mit der die Augenzahl ,,6'' bzw. ,,1''
beim zweimaligen Würfeln erzielt wird; vgl.
Abschnitt 3.3.1. Dann ergeben sich die folgenden bedingten
Wahrscheinichkeitsfunktionen von  unter der Bedingung
unter der Bedingung 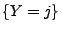 :
:
- integrierte Gleichverteilung
Sei 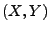 ein absolutstetiger Zufallsvektor mit der
gemeinsamen Dichte
Für
ein absolutstetiger Zufallsvektor mit der
gemeinsamen Dichte
Für ![$ y\in(0,1]$](img818.png) gilt dann für die bedingte Dichte von
gilt dann für die bedingte Dichte von  unter der Bedingung
unter der Bedingung
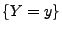 :
Die bedingte Dichte
:
Die bedingte Dichte
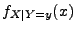 stimmt also bei
diesem Beispiel mit der
(unbedingten Rand-)Dichte
stimmt also bei
diesem Beispiel mit der
(unbedingten Rand-)Dichte 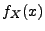 von
von  überein; vgl.
Abschnitt 3.3.3.
überein; vgl.
Abschnitt 3.3.3.




Next: Unabhängige Zufallsvariablen
Up: Zufallsvektoren
Previous: Weitere Beispiele von Zufallsvektoren
Contents
Ursa Pantle
2004-05-10
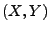 ein diskreter Zufallsvektor mit
ein diskreter Zufallsvektor mit
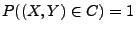 für
eine abzählbare Menge
für
eine abzählbare Menge
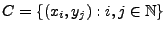 .
.
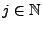 mit
mit
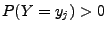 heißt dann
heißt dann
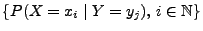 die bedingte
Wahrscheinlichkeitsfunktion von
die bedingte
Wahrscheinlichkeitsfunktion von  unter der Bedingung
unter der Bedingung
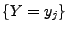 .
.
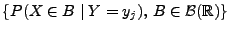 von
von  unter der Bedingung
unter der Bedingung 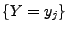 eindeutig.
eindeutig.
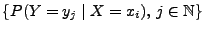 bzw.
bzw.
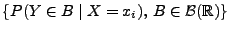 für jedes
für jedes
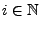 mit
mit
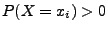 die bedingte Wahrscheinlichkeitsfunktion bzw. bedingte Verteilung
von
die bedingte Wahrscheinlichkeitsfunktion bzw. bedingte Verteilung
von 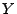 unter der Bedingung
unter der Bedingung  .
.
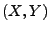 ein absolutstetiger Zufallsvektor mit der
gemeinsamen Dichte
ein absolutstetiger Zufallsvektor mit der
gemeinsamen Dichte
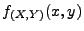 .
.
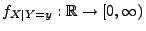 mit
die bedingte Dichte von
mit
die bedingte Dichte von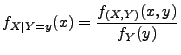
 unter der Bedingung
unter der Bedingung
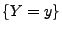 , wobei
, wobei 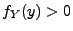 vorausgesetzt wird.
vorausgesetzt wird.
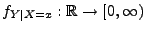 mit
die bedingte Dichte von
mit
die bedingte Dichte von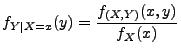
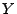 unter der Bedingung
unter der Bedingung 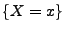 ,
wobei
,
wobei 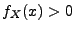 vorausgesetzt wird.
vorausgesetzt wird.
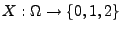 bzw.
bzw.
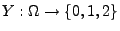 die (zufällige) Anzahl, mit der die Augenzahl ,,6'' bzw. ,,1''
beim zweimaligen Würfeln erzielt wird; vgl.
Abschnitt 3.3.1. Dann ergeben sich die folgenden bedingten
Wahrscheinichkeitsfunktionen von
die (zufällige) Anzahl, mit der die Augenzahl ,,6'' bzw. ,,1''
beim zweimaligen Würfeln erzielt wird; vgl.
Abschnitt 3.3.1. Dann ergeben sich die folgenden bedingten
Wahrscheinichkeitsfunktionen von  unter der Bedingung
unter der Bedingung 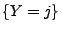 :
:
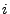
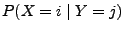
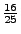
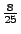
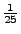
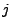
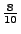
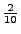
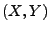 ein absolutstetiger Zufallsvektor mit der
gemeinsamen Dichte
Für
ein absolutstetiger Zufallsvektor mit der
gemeinsamen Dichte
Für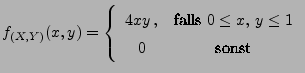
![$ y\in(0,1]$](img818.png) gilt dann für die bedingte Dichte von
gilt dann für die bedingte Dichte von  unter der Bedingung
unter der Bedingung
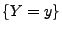 :
Die bedingte Dichte
:
Die bedingte Dichte![$\displaystyle f_{X\mid Y=y}(x)=\frac{f_{(X,Y)}(x,y)}{f_Y(y)}=
\left\{\begin{array}{cc}
2x\,,&\mbox{falls $x\in[0,1]$}\\
0&\mbox{sonst}
\end{array}\right.
$](img819.png)
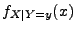 stimmt also bei
diesem Beispiel mit der
(unbedingten Rand-)Dichte
stimmt also bei
diesem Beispiel mit der
(unbedingten Rand-)Dichte 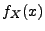 von
von  überein; vgl.
Abschnitt 3.3.3.
überein; vgl.
Abschnitt 3.3.3.