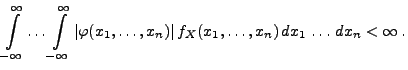Next: Multiplikationsformel und Kovarianz
Up: Gemischte Momente
Previous: Gemischte Momente
Contents
Transformationssatz für Zufallsvektoren
Auf die gleiche Weise wie Theorem 4.7, d.h. mittels
algebraischer Induktion, ergibt sich der folgende
Transformationssatz für Zufallsvektoren.
Theorem 4.8
Sei
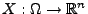
ein beliebiger
Zufallsvektor, und sei
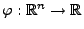
eine
Borel-messbare Abbildung, so dass
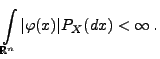 |
(35) |
Für den Erwartungswert
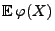
von
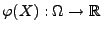
gilt dann
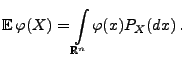 |
(36) |
Die Aussage von Theorem 4.8 lässt sich wie folgt für
diskrete bzw. absolutstetige Zufallsvektoren spezifizieren
(genauso wie dies im eindimensionalen Fall in
Korollar 4.3 getan wurde).
Korollar 4.4
Sei
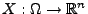
ein beliebiger
Zufallsvektor, und sei
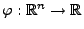
eine
beliebige Borel-messbare Abbildung.
- 1.
 Falls
Falls  diskret ist mit
diskret ist mit
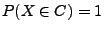 für eine
abzählbare Menge
für eine
abzählbare Menge
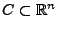 , dann gilt
, dann gilt
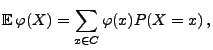 |
(37) |
wobei vorausgesetzt wird, dass
- 2.
 Falls
Falls  absolutstetig ist mit der (gemeinsamen) Dichte
absolutstetig ist mit der (gemeinsamen) Dichte 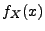 ,
dann gilt
,
dann gilt
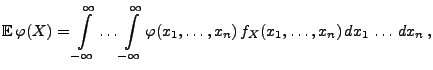 |
(38) |
wobei vorausgesetzt wird, dass
Der Beweis von Korollar 4.4 verläuft analog zum
Beweis von Korollar 4.3. Er wird deshalb
weggelassen.




Next: Multiplikationsformel und Kovarianz
Up: Gemischte Momente
Previous: Gemischte Momente
Contents
Ursa Pantle
2004-05-10