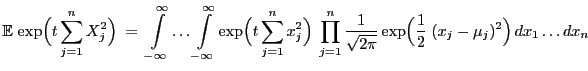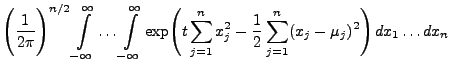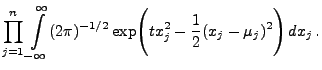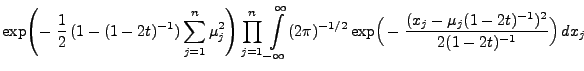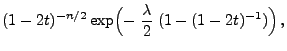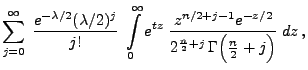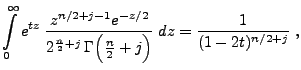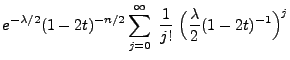Nächste Seite: Verteilungs- und Unabhängigkeitseigenschaften linearer
Aufwärts: Lineare und quadratische Formen
Vorherige Seite: Definition, Erwartungswert und Kovarianz
Inhalt
Nichtzentrale  -Verteilung
-Verteilung
Um die Verteilung von quadratischen Formen normalverteilter
Zufallsvektoren zu bestimmen, führen wir die (parametrische)
Familie der nichtzentralen  -Verteilungen ein.
-Verteilungen ein.
- Definition
 Sei
Sei
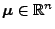 und
und
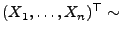 N
N
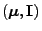 . Dann sagt man, dass die Zufallsvariable
eine nichtzentrale
. Dann sagt man, dass die Zufallsvariable
eine nichtzentrale  -Verteilung mit
-Verteilung mit  Freiheitsgraden und dem Nichtzentralitätsparameter
Freiheitsgraden und dem Nichtzentralitätsparameter
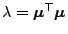 hat. (Schreibweise:
hat. (Schreibweise:
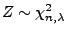 )
)
- Beachte
-
- Für
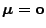 ergibt sich als Spezialfall die bereits in
Abschnitt I-1.3.1 eingeführte (zentrale)
ergibt sich als Spezialfall die bereits in
Abschnitt I-1.3.1 eingeführte (zentrale)  -Verteilung
-Verteilung
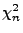 mit
mit  Freiheitsgraden.
Freiheitsgraden.
- Um eine Formel für die Dichte der nichtzentralen
 -Verteilung herzuleiten, betrachten wir (neben der
charakteristischen Funktion) noch eine weitere Integraltransformation von Wahrscheinlichkeitsdichten.
-Verteilung herzuleiten, betrachten wir (neben der
charakteristischen Funktion) noch eine weitere Integraltransformation von Wahrscheinlichkeitsdichten.
- Definition
-
Es gilt der folgende Eindeutigkeitssatz für momenterzeugende
Funktionen, den wir hier ohne Beweis angeben.
Lemma 1.12
- Seien
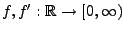 die Dichten von reellwertigen
Zufallsvariablen, und seien die zugehörigen momenterzeugenden
Funktionen
die Dichten von reellwertigen
Zufallsvariablen, und seien die zugehörigen momenterzeugenden
Funktionen
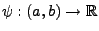 bzw.
bzw.
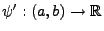 auf
einem (gemeinsamen) Intervall
auf
einem (gemeinsamen) Intervall 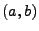 mit
mit 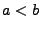 wohldefiniert.
wohldefiniert.
- Es gilt
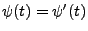 für jedes
für jedes 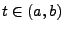 genau dann,
wenn
genau dann,
wenn
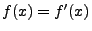 für fast jedes
für fast jedes
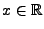 .
.
Mit Hilfe von Lemma 1.12 können wir nun die Dichte
der nichtzentralen  -Verteilung bestimmen.
-Verteilung bestimmen.
- Beweis
-




Nächste Seite: Verteilungs- und Unabhängigkeitseigenschaften linearer
Aufwärts: Lineare und quadratische Formen
Vorherige Seite: Definition, Erwartungswert und Kovarianz
Inhalt
Hendrik Schmidt
2006-02-27
![]() -Verteilungen ein.
-Verteilungen ein.
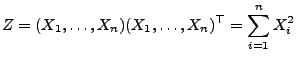
![]() -Verteilung bestimmen.
-Verteilung bestimmen.