Nächste Seite: Lineare Modelle; Designmatrix mit
Aufwärts: Lineare und quadratische Formen
Vorherige Seite: Nichtzentrale -Verteilung
Inhalt
Verteilungs- und Unabhängigkeitseigenschaften
linearer und quadratischer Formen
Die Verteilungseigenschaft (33) für quadratische
Formen von normalverteilten Zufallsvektoren lässt sich wie folgt
verallgemeinern. Dabei ist Lemma 1.7 über die
Faktorisierung symmetrischer und nichtnegativ definiter Matrizen
nützlich.
Theorem 1.9
- Sei
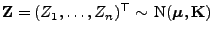 ,
wobei die Kovarianzmatrix
,
wobei die Kovarianzmatrix
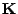 positiv definit sei. Außerdem
sei
positiv definit sei. Außerdem
sei
 eine symmetrische
eine symmetrische 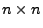 Matrix mit
Matrix mit
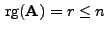 .
.
- Wenn die Matrix
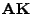 idempotent ist, d.h., wenn
idempotent ist, d.h., wenn
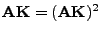 , dann gilt
, dann gilt
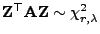 , wobei
, wobei
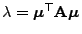 .
.
- Beweis
-
- Die Matrix
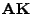 sei idempotent. Dann gilt
sei idempotent. Dann gilt
- Weil
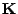 regulär ist, kann man beide Seiten dieser Gleichung
von rechts mit
regulär ist, kann man beide Seiten dieser Gleichung
von rechts mit
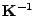 multiplizieren. Dabei ergibt sich,
dass
multiplizieren. Dabei ergibt sich,
dass
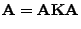 |
(34) |
bzw. für jedes
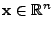 d.h.,
d.h.,
 ist nichtnegativ definit.
ist nichtnegativ definit.
- Gemäß Lemma 1.7 gibt es somit eine Zerlegung
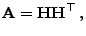 |
(35) |
so dass die 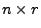 Matrix
Matrix
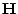 den
vollen Spaltenrang
den
vollen Spaltenrang 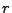 hat.
hat.
- Wegen Lemma 1.2 bedeutet dies, dass die inverse
Matrix
 existiert.
existiert.
- Aus Theorem 1.3 über die lineare Transformation von
normalverteilten Zufallvektoren ergibt sich nun für den
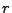 -dimensionalen Vektor
-dimensionalen Vektor
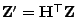 , dass
, dass
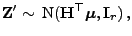 |
(36) |
weil
wobei sich die letzten drei Gleichheiten aus (34)
bzw. (35) ergeben.
- Weil andererseits
und weil
ergibt sich die Behauptung nun aus (36) und aus der
Definition der nichtzentralen
 -Verteilung.
-Verteilung.

Außerdem ist das folgende Kriterium für die Unabhängigkeit von
linearen bzw. quadratischen Formen normalverteilter
Zufallsvektoren nützlich. Es kann als (vektorielle)
Verallgemeinerung von Lemma 5.3 im Skript zur Vorlesung
,,Statistik I'' aufgefasst werden.
- Beweis
-
- Wir zeigen zunächst, dass aus (37) die
Unabhängigkeit der linearen Formen
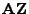 und
und
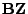 folgt.
folgt.
- Wegen des Eindeutigkeitssatzes für charakteristische Funktionen
von Zufallsvektoren (vgl. Lemma 1.9) genügt es zu
zeigen, dass für beliebige
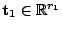 ,
,
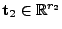
- Aus (37) folgt, dass
und somit auch, dass für beliebige
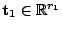 ,
,
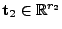
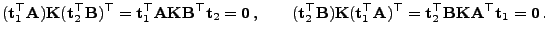 |
(38) |
- Aus der in Theorem 1.4 hergeleiteten
Darstellungsformel (25) für die charakteristische
Funktion von normalverteilten Zufallsvektoren und aus
(38) ergibt sich dann, dass
- Wir zeigen nun noch, dass die Unabhängigkeit von
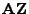 und
und
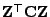 aus der zweiten Bedingung in
(37) folgt.
aus der zweiten Bedingung in
(37) folgt.
- Sei
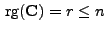 . Gemäß Lemma 1.7 gibt es
dann eine
. Gemäß Lemma 1.7 gibt es
dann eine 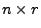 Matrix
Matrix
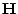 mit
mit
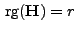 , so dass
, so dass
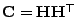 .
.
- Aus (37) ergibt sich dann, dass
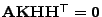 bzw.
bzw.
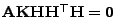 .
.
- Hieraus folgt schließlich, dass
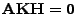 , weil
die
, weil
die 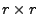 Matrix
Matrix
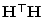 wegen
Lemma 1.2 den (vollen) Rang
wegen
Lemma 1.2 den (vollen) Rang
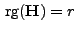 hat und
deshalb invertierbar ist.
hat und
deshalb invertierbar ist.
- Aus dem ersten Teil des Beweises ergibt sich somit, dass die
linearen Formen
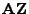 und
und
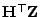 unabhängig
sind.
unabhängig
sind.
- Wegen
ergibt sich nun aus dem Transformationssatz für unabhängige
Zufallsvektoren (vgl. Theorem I-1.8), dass auch
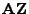 und
und
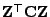 unabhängig sind.
unabhängig sind.





Nächste Seite: Lineare Modelle; Designmatrix mit
Aufwärts: Lineare und quadratische Formen
Vorherige Seite: Nichtzentrale -Verteilung
Inhalt
Hendrik Schmidt
2006-02-27