



Nächste Seite: Eigenwerte und Eigenvektoren
Aufwärts: Einige Grundbegriffe und Ergebnisse
Vorherige Seite: Einige Grundbegriffe und Ergebnisse
Inhalt
Spur und Rang
Unmittelbar aus der Definitionsgleichung (1) der
Matix-Spur und aus der Definition der Matrix-Multiplikation
ergibt sich der folgende Hilfssatz.
Lemma 1.1

Sei
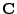
eine beliebige
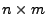
Matrix und
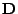
eine beliebige
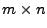
Matrix. Dann gilt
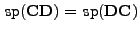
.
Man kann zeigen, dass eine quadratische Matrix
 genau dann
invertierbar ist, wenn
genau dann
invertierbar ist, wenn
 vollen Rang hat bzw. wenn
vollen Rang hat bzw. wenn
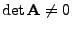 gilt. In diesem Zusammenhang ist auch das folgende
Rsultat nützlich.
gilt. In diesem Zusammenhang ist auch das folgende
Rsultat nützlich.
Lemma 1.2
Sei

eine
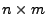
Matrix mit
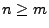
und
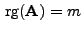
. Dann gilt
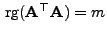
.
- Beweis
-
- Es ist klar, dass der Rang
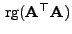 der
der 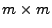 Matrix
Matrix
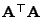 nicht größer als
nicht größer als 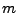 sein kann.
sein kann.
- Wir nehmen nun an, dass
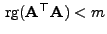 . Dann gibt es
einen Vektor
. Dann gibt es
einen Vektor
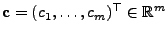 , so dass
, so dass
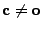 und
und
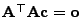 .
.
- Hieraus folgt, dass auch
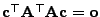 bzw.
bzw.
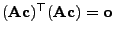 , d.h.
, d.h.
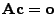 .
.
- Dies ist jedoch ein Widerspruch zu der Voraussetzung, dass
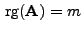 .
.

Außerdem kann man zeigen, dass die beiden folgenden Eigenschaften
von Spur bzw. Rang gelten.
Lemma 1.3

Seien

und
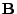
beliebige
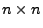
Matrizen.
Dann gilt stets
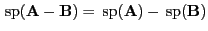
.
Wenn

idempotent und symmetrisch ist, d.h.,
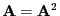
und

, dann gilt außerdem
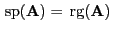
.




Nächste Seite: Eigenwerte und Eigenvektoren
Aufwärts: Einige Grundbegriffe und Ergebnisse
Vorherige Seite: Einige Grundbegriffe und Ergebnisse
Inhalt
Hendrik Schmidt
2006-02-27
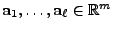 linear abhängig, wenn es reelle Zahlen
linear abhängig, wenn es reelle Zahlen
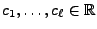 gibt, die nicht alle gleich Null sind, so dass
gibt, die nicht alle gleich Null sind, so dass
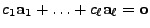 .
.
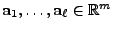 linear unabhängig.
linear unabhängig.
![]() genau dann
invertierbar ist, wenn
genau dann
invertierbar ist, wenn
![]() vollen Rang hat bzw. wenn
vollen Rang hat bzw. wenn
![]() gilt. In diesem Zusammenhang ist auch das folgende
Rsultat nützlich.
gilt. In diesem Zusammenhang ist auch das folgende
Rsultat nützlich.