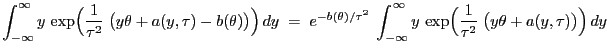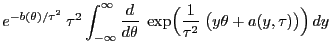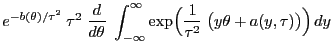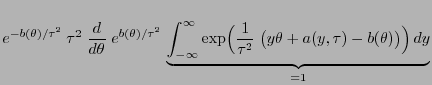Nächste Seite: Verknüpfung der Parameter; natürliche
Aufwärts: Definition und grundlegende Eigenschaften
Vorherige Seite: Definition und grundlegende Eigenschaften
Inhalt
Exponentialfamilie
Wir nehmen an, dass die Stichprobenvariablen
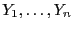 unabhängig (jedoch i. a. nicht identisch verteilt) sind,
unabhängig (jedoch i. a. nicht identisch verteilt) sind,
- Beachte
-
Im absolutstetigen Fall kann der Störparameter
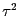 die Rolle
eines zusätzlichen Varianzparameters spielen, während
die Rolle
eines zusätzlichen Varianzparameters spielen, während 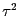 im
diskreten Fall meistens gleich
im
diskreten Fall meistens gleich 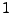 gesetzt wird.
gesetzt wird.
Lemma 4.1
Der in
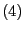
bzw.
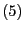
gegebene Parameterraum
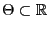
ist ein Intervall in
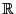
.
- Beweis
-
Wegen Lemma 4.1 können (und werden) wir in diesem
Kapitel stets annehmen, dass
 ein offenes
Intervall ist, so dass die Integrierbarkeitsbedingung in
(4) bzw. (5) für jedes
ein offenes
Intervall ist, so dass die Integrierbarkeitsbedingung in
(4) bzw. (5) für jedes
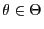 erfüllt ist.
erfüllt ist.
- Beweis
-
- Wir betrachten erneut lediglich den absolutstetigen Fall, denn im
diskreten Fall verläuft der Beweis analog. Dabei gilt
- Auf ähnliche Weise ergibt sich, dass
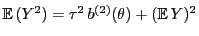 .
.





Nächste Seite: Verknüpfung der Parameter; natürliche
Aufwärts: Definition und grundlegende Eigenschaften
Vorherige Seite: Definition und grundlegende Eigenschaften
Inhalt
Hendrik Schmidt
2006-02-27
![]() unabhängig (jedoch i. a. nicht identisch verteilt) sind,
unabhängig (jedoch i. a. nicht identisch verteilt) sind,
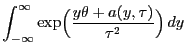
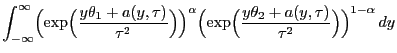
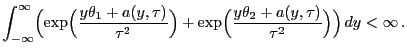
![]() ein offenes
Intervall ist, so dass die Integrierbarkeitsbedingung in
(4) bzw. (5) für jedes
ein offenes
Intervall ist, so dass die Integrierbarkeitsbedingung in
(4) bzw. (5) für jedes
![]() erfüllt ist.
erfüllt ist.