



Nächste Seite: Beispiele
Aufwärts: Definition und grundlegende Eigenschaften
Vorherige Seite: Exponentialfamilie
Inhalt
Verknüpfung der Parameter; natürliche Linkfunktion
- Beachte
-
Die Linkfunktion
 heißt natürlich, wenn
heißt natürlich, wenn 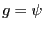 .
In diesem Fall gilt
.
In diesem Fall gilt
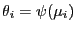 bzw.
bzw.
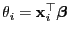 für jedes
für jedes
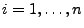 , d.h.,
, d.h.,
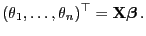 |
(13) |




Nächste Seite: Beispiele
Aufwärts: Definition und grundlegende Eigenschaften
Vorherige Seite: Exponentialfamilie
Inhalt
Hendrik Schmidt
2006-02-27