



Nächste Seite: Asymptotische Verteilung
Aufwärts: Kolmogorow-Smirnow-Test
Vorherige Seite: Kolmogorow-Smirnow-Test
Inhalt
Empirische Verteilungsfunktion;
KS-Teststatistik
- Beachte
-
- Die Quantile
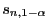 lassen sich durch
Monte-Carlo-Simulation bestimmen, wobei die Verteilungsfunktion
lassen sich durch
Monte-Carlo-Simulation bestimmen, wobei die Verteilungsfunktion
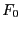 der Standard-Gleichverteilung in
der Standard-Gleichverteilung in ![$ [0,1]$](img1880.png) zugrunde gelegt
werden kann, vgl. Korollar I-1.3.
zugrunde gelegt
werden kann, vgl. Korollar I-1.3.
- Wenn nicht vorausgesetzt wird, dass
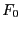 stetig ist, dann liefert
die in (3) betrachtete Entscheidungsregel einen
Test, dessen Niveau kleiner als
stetig ist, dann liefert
die in (3) betrachtete Entscheidungsregel einen
Test, dessen Niveau kleiner als 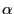 sein kann.
sein kann.
- Wenn jedoch das Quantil
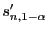 von
von
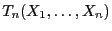 unter
unter 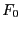 (beispielsweise durch
MC-Simulation) bestimmt werden kann, dann ist durch
(beispielsweise durch
MC-Simulation) bestimmt werden kann, dann ist durch
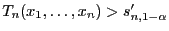 auch bei unstetigem
auch bei unstetigem
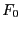 ein Test gegeben, der das Niveau
ein Test gegeben, der das Niveau 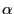 ausschöpft.
ausschöpft.




Nächste Seite: Asymptotische Verteilung
Aufwärts: Kolmogorow-Smirnow-Test
Vorherige Seite: Kolmogorow-Smirnow-Test
Inhalt
Hendrik Schmidt
2006-02-27