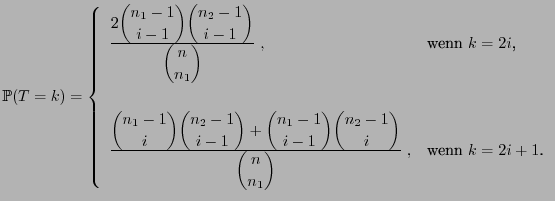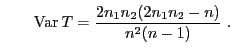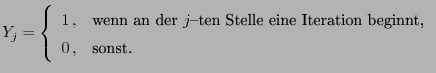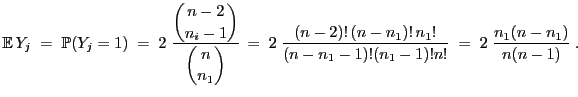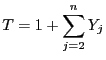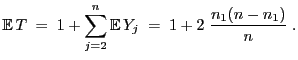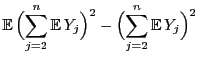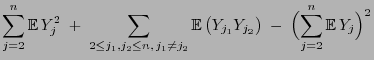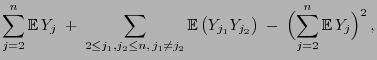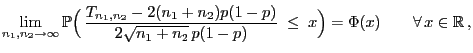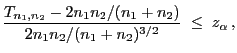Nächste Seite: Vorzeichenrangtest von Wilcoxon
Aufwärts: Zwei einfache Beispiele von
Vorherige Seite: Binomialtest
Inhalt
Iterationstest auf Zufälligkeit
- In diesem Abschnitt wird nicht vorausgesetzt, dass die
Stichprobenvariablen
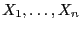 unabhängig sind.
unabhängig sind.
- Wir nehmen nämlich an, dass
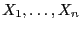 nur die Werte 0
oder
nur die Werte 0
oder 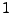 annehmen können, wobei
annehmen können, wobei 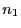 -mal der Wert 0 und
-mal der Wert 0 und
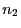 -mal der Wert
-mal der Wert 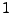 auftreten möge;
auftreten möge; 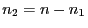 .
.
- Insgesamt gibt es dann
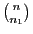 mögliche Realisierungen
der Zufallsstichprobe
mögliche Realisierungen
der Zufallsstichprobe
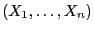 .
.
- Dabei soll die Nullhypothese
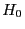 geprüft werden, ob jede dieser
geprüft werden, ob jede dieser
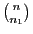 Realisierungen die gleiche Wahrscheinlichkeit
hat.
Realisierungen die gleiche Wahrscheinlichkeit
hat.
- Mit anderen Worten: Es soll geprüft werden, ob die Lokalisation,
d.h. die Reihenfolge ,,rein zufällig'' ist, in der die
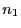 Einsen bzw. die
Einsen bzw. die 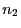 Nullen angeordnet sind.
Nullen angeordnet sind.
- Als Testgröße
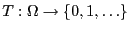 betrachten wir die
Anzahl
betrachten wir die
Anzahl 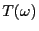 von Iterationen in der (konkreten)
Stichprobe
von Iterationen in der (konkreten)
Stichprobe
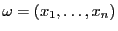 , d.h. die Anzahl von (Teil-)
Folgen aufeinanderfolgender gleicher Zeichen in
, d.h. die Anzahl von (Teil-)
Folgen aufeinanderfolgender gleicher Zeichen in
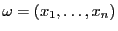 .
.
- Beispiel
-
Theorem 6.1

Unter
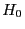
gilt für jedes
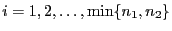
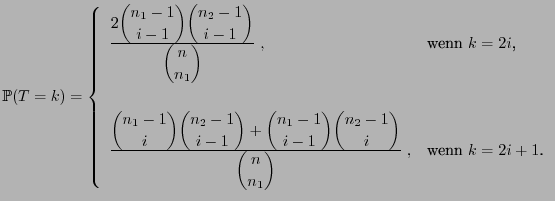 |
(3) |
Außerdem gilt
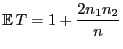 und und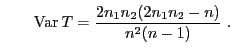 |
(4) |
- Beweis
-
- Wir zeigen die Gültigkeit von (3) nur für den Fall
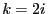 , denn der Beweis für den Fall
, denn der Beweis für den Fall 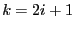 verläuft analog.
verläuft analog.
- Sei also
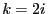 . Dann gibt es je
. Dann gibt es je 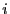 Iterationen, die aus Einsen
bzw. aus Nullen bestehen.
Iterationen, die aus Einsen
bzw. aus Nullen bestehen.
- Für die Zerlegung der
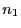 Nullen in
Nullen in 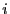 Teilmengen gibt es
Teilmengen gibt es
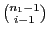 Möglichkeiten.
Möglichkeiten.
- Für jede dieser Zerlegungen gibt es
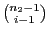 Möglichkeiten, die
Möglichkeiten, die 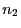 Einsen in
Einsen in 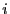 Teilmengen zu zerlegen.
Teilmengen zu zerlegen.
- Wenn nun noch beachtet wird, dass die Stichprobe
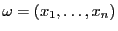 entweder mit
entweder mit 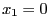 oder mit
oder mit 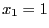 beginnen kann, dann ergeben sich insgesamt
beginnen kann, dann ergeben sich insgesamt
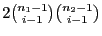 Zerlegungsmöglichkeiten.
Zerlegungsmöglichkeiten.
- Damit ist (3) für den Fall
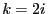 bewiesen.
bewiesen.
- Bei der Bestimmung des Erwartungswertes
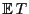 nutzen wir die
folgende Überlegung.
nutzen wir die
folgende Überlegung.
- Für jedes
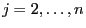 betrachten wir die Indikatorvariable
betrachten wir die Indikatorvariable
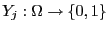 mit
mit
- Dann gilt
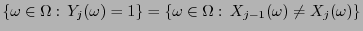 , d.h., es gibt
, d.h., es gibt
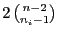 Möglichkeiten, dass an der
Möglichkeiten, dass an der 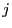 -ten Stelle eine Iteration beginnt.
-ten Stelle eine Iteration beginnt.
- Somit gilt
- Hieraus und aus der Identität
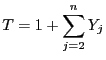 |
(5) |
ergibt sich, dass
- Die Varianzformel in (4) lässt sich auf ähnliche
Weise beweisen, denn aus (5) ergibt sich, dass
so dass lediglich noch die Momente
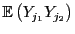 zu bestimmen sind.
zu bestimmen sind.

- Beachte
-
- Beispiel
 (Fortsetzung)
(Fortsetzung) Für
Für
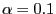 und
und 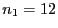 ,
, 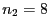 ergibt sich, dass
ergibt sich, dass
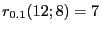 . Andererseits gilt für die in
(2) betrachtete Stichprobe
d.h.,
. Andererseits gilt für die in
(2) betrachtete Stichprobe
d.h., 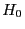 wird abgelehnt.
wird abgelehnt.
Wenn die (Teil-) Stichprobenumfänge 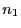 und
und 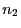 groß sind,
dann ist die Bestimmung der Quantile
groß sind,
dann ist die Bestimmung der Quantile
 von
von
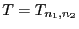 mit erheblichem Rechenaufwand verbunden. Einen
Ausweg bietet dann der folgenden zentrale Grenzwertsatz, den wir
hier ohne Beweis angeben.
mit erheblichem Rechenaufwand verbunden. Einen
Ausweg bietet dann der folgenden zentrale Grenzwertsatz, den wir
hier ohne Beweis angeben.
Theorem 6.2

Wenn
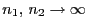
, so
dass
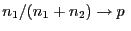
bzw.
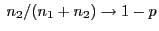
für ein
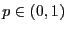
, dann gilt
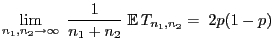 und und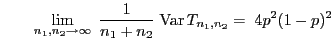 |
(6) |
sowie
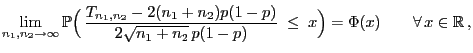 |
(7) |
wobei
![$ \Phi:\mathbb{R}\to[0,1]$](img2087.png)
die Verteilungsfunktion der
N
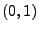
-Verteilung ist.
- Beachte
 Wegen Theorem 6.2 wird
Wegen Theorem 6.2 wird 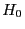 für
große
für
große  abgelehnt, wenn
abgelehnt, wenn
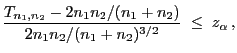 |
(8) |
wobei 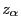 das
das 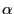 -Quantil der N
-Quantil der N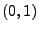 -Verteilung
ist.
-Verteilung
ist.




Nächste Seite: Vorzeichenrangtest von Wilcoxon
Aufwärts: Zwei einfache Beispiele von
Vorherige Seite: Binomialtest
Inhalt
Hendrik Schmidt
2006-02-27
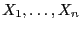 nur die Werte 0
oder
nur die Werte 0
oder 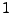 annehmen können, wobei
annehmen können, wobei 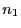 -mal der Wert 0 und
-mal der Wert 0 und
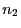 -mal der Wert
-mal der Wert 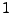 auftreten möge;
auftreten möge; 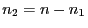 .
.
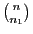 mögliche Realisierungen
der Zufallsstichprobe
mögliche Realisierungen
der Zufallsstichprobe
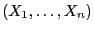 .
.
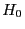 geprüft werden, ob jede dieser
geprüft werden, ob jede dieser
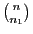 Realisierungen die gleiche Wahrscheinlichkeit
hat.
Realisierungen die gleiche Wahrscheinlichkeit
hat.
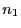 Einsen bzw. die
Einsen bzw. die 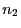 Nullen angeordnet sind.
Nullen angeordnet sind.