Nächste Seite: Iterationstest auf Zufälligkeit
Aufwärts: Zwei einfache Beispiele von
Vorherige Seite: Zwei einfache Beispiele von
Inhalt
Binomialtest
- Der in Abschnitt 5.2 betrachtete
 -Anpassungstest kann durch den folgenden Binomialtest ersetzt werden, wenn
-Anpassungstest kann durch den folgenden Binomialtest ersetzt werden, wenn 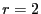 , d.h., wenn nur zwei
Klassen betrachtet werden (beispielsweise bei binären
Alternativdaten).
, d.h., wenn nur zwei
Klassen betrachtet werden (beispielsweise bei binären
Alternativdaten).
- Wir zerlegen also den Wertebereich der (unabhängigen und identisch
verteilten) Stichprobenvariablen
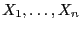 in zwei
Teilmengen
in zwei
Teilmengen ![$ (a_1,b_1]$](img2342.png) und
und ![$ (a_2,b_2]$](img2343.png) , so dass
, so dass
![$\displaystyle (a_1,b_1]\cap
(a_2,b_2]=\emptyset$](img2344.png)
und
![$\displaystyle \qquad\mathbb{P}\bigl(X_1\in
(a_1,b_1]\cup (a_2,b_2]\bigr)=1 ,
$](img2345.png)
und betrachten die ,,Klassenstärke''
- Man kann sich leicht überlegen, dass
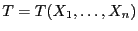 binomialverteilt ist, d.h.,
binomialverteilt ist, d.h.,
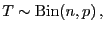 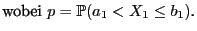 |
(1) |
- Wir betrachten zunächst das Testproblem
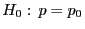 versus
versus
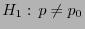 , wobei
, wobei
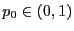 eine beliebige positive
Zahl ist.
eine beliebige positive
Zahl ist.
- Das (einseitige) Testproblem
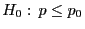 versus
versus
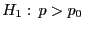 kann ähnlich behandelt werden. Dabei wird
kann ähnlich behandelt werden. Dabei wird 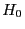 abgelehnt, wenn
abgelehnt, wenn
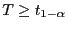 .
.
- Völlig analog ergibt sich eine Enscheidungsregel für das
(einseitige) Testproblem
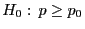 versus
versus
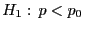 ,
wobei
,
wobei 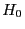 abgelehnt wird, wenn
abgelehnt wird, wenn
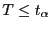 .
.
- Beachte
-
- Der oben beschriebene Binomialtest wird auch Vorzeichentest
genannt, weil die Bildung von 2 Klassen als Binarisierung der
ursprünglich vorliegenden Daten aufgefasst werden kann.
- Bei den beiden einseitigen Testproblemen erfolgt die Bestimmung
der kritischen Werte
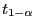 bzw.
bzw. 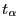 für
für 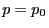 ,
obwohl die Nullhypothese
,
obwohl die Nullhypothese
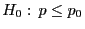 bzw.
bzw.
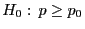 lautet.
lautet.
- Die Tatsache, dass dennoch die Werte
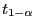 bzw.
bzw.
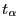 betrachtet werden, steht nicht damit im Widerspruch,
dass für jedes einzelne
betrachtet werden, steht nicht damit im Widerspruch,
dass für jedes einzelne 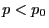 bzw.
bzw. 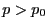 der kritische Wert
kleiner als
der kritische Wert
kleiner als
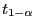 bzw. größer als
bzw. größer als 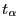 wäre und
dass dann
wäre und
dass dann 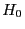 öfter abgelehnt werden müsste.
öfter abgelehnt werden müsste.
- Die Erklärung für die Wahl der kritischen Werte
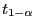 bzw.
bzw. 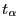 ist, dass nicht ein einzelnes
ist, dass nicht ein einzelnes 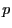 mit
mit 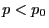 bzw.
bzw.
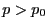 betrachtet wird, sondern dass
betrachtet wird, sondern dass 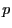 beliebig nahe bei
beliebig nahe bei 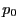 liegen kann und dass insbesondere auch
liegen kann und dass insbesondere auch 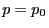 zugelassen wird.
zugelassen wird.
- Wenn der Stichprobenumfang
 groß ist und wenn
groß ist und wenn 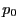 nahe bei
0 oder
nahe bei
0 oder 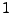 liegt,
liegt,
- dann ist die direkte Berechnung der Quantile
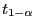 bzw.
bzw.
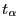 der Binomialverteilung Bin
der Binomialverteilung Bin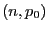 schwierig.
schwierig.
- Aus dem Gesetz der seltenen Ereignisse (vgl. Abschnitt WR-3.2.2)
ergibt sich, dass
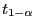 bzw.
bzw. 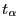 in diesem Fall
durch Quantile der Poisson-Verteilung Poi
in diesem Fall
durch Quantile der Poisson-Verteilung Poi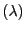 approximiert
werden können, wobei
approximiert
werden können, wobei
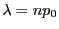 bzw.
bzw.
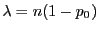 .
.
- Außerdem kann
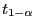 bzw.
bzw. 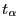 für jedes beliebige
für jedes beliebige
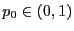 durch geeignet transformierte Quantile der
N
durch geeignet transformierte Quantile der
N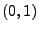 -Verteilung approximiert werden können, wenn der
Stichprobenumfang
-Verteilung approximiert werden können, wenn der
Stichprobenumfang  ,,hinreichend groß'' ist.
,,hinreichend groß'' ist.
- Als ein mögliches Kriterium für ,,hinreichend groß'' werden dabei
in der Literatur beispielsweise die Bedingungen
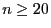 und
und
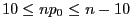 angegeben.
angegeben.
- Beispiel
-




Nächste Seite: Iterationstest auf Zufälligkeit
Aufwärts: Zwei einfache Beispiele von
Vorherige Seite: Zwei einfache Beispiele von
Inhalt
Hendrik Schmidt
2006-02-27
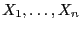 in zwei
Teilmengen
in zwei
Teilmengen ![$ (a_1,b_1]$](img2342.png) und
und ![$ (a_2,b_2]$](img2343.png) , so dass
und betrachten die ,,Klassenstärke''
, so dass
und betrachten die ,,Klassenstärke''![$\displaystyle (a_1,b_1]\cap
(a_2,b_2]=\emptyset$](img2344.png) und
und![$\displaystyle \qquad\mathbb{P}\bigl(X_1\in
(a_1,b_1]\cup (a_2,b_2]\bigr)=1 ,
$](img2345.png)
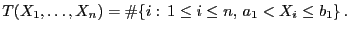
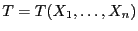 binomialverteilt ist, d.h.,
binomialverteilt ist, d.h.,
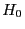 abgelehnt, wenn
abgelehnt, wenn
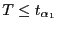 oder
oder
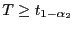 ,
,
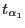 und
und
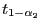 für beliebige
für beliebige
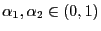 mit
mit
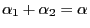 gegeben sind durch
gegeben sind durch
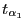
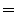
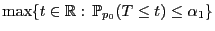
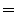
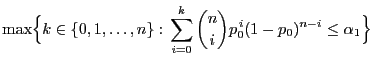
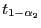
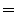
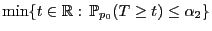
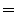
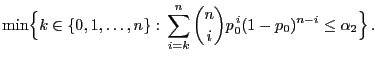
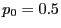 wird dabei normalerweise
wird dabei normalerweise
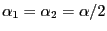 gewählt. Wenn
gewählt. Wenn 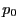 nahe bei 0 bzw.
nahe bei 0 bzw.
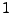 liegt, dann ist es zweckmäßig
liegt, dann ist es zweckmäßig 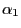 kleiner bzw. größer
als
kleiner bzw. größer
als 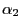 zu wählen.
zu wählen.
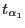 bzw.
bzw.
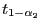 der
Binomialverteilung Bin
der
Binomialverteilung Bin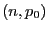 können entweder aus Tabellen
entnommen oder per Monte-Carlo-Simulation bestimmt werden.
können entweder aus Tabellen
entnommen oder per Monte-Carlo-Simulation bestimmt werden.