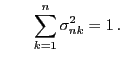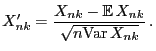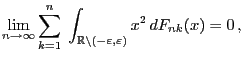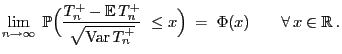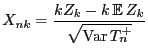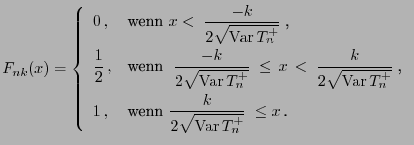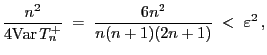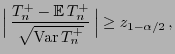Nächste Seite: Zweistichproben-Probleme
Aufwärts: Vorzeichenrangtest von Wilcoxon
Vorherige Seite: Verteilung der Teststatistik für
Inhalt
Asymptotische Verteilung
- Wenn der Stichprobenumfang
 groß ist, dann ist die direkte
Bestimmung der Quantile
groß ist, dann ist die direkte
Bestimmung der Quantile
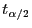 und
und
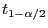 mit
Hilfe von Theorem 6.3 schwierig.
mit
Hilfe von Theorem 6.3 schwierig.
- Ein anderer Zugang zur (näherungsweisen) Bestimmung der Verteilung
der Teststatistik
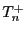 beruht auf der Darstellungsformel
(14).
beruht auf der Darstellungsformel
(14).
- Dabei wird die Tatsache genutzt, dass
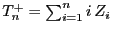 wegen Lemma 6.1 eine Summe von unabhängigen
Zufallsvariablen ist.
wegen Lemma 6.1 eine Summe von unabhängigen
Zufallsvariablen ist.
- Und zwar kann mit Hilfe eines zentralen Grenzwertsatzes für Summen
von unabhängigen (jedoch nicht notwendig identisch verteilten)
Zufallsvariablen gezeigt werden, dass
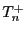 asymptotisch
normalverteilt ist.
asymptotisch
normalverteilt ist.
- Hierfür betrachten wir das folgende stochastische Modell: Für
jedes
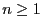 sei
sei
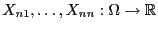 eine Folge
von unabhängigen Zufallsvariablen,
eine Folge
von unabhängigen Zufallsvariablen,
Der folgende zentrale Grenzwertsatz von Lindeberg
(vgl.Theorem WR-5.22) bildet die Grundlage, um zu zeigen, dass
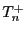 asymptotisch normalverteilt ist.
asymptotisch normalverteilt ist.
- Beweis
-
- Wegen (14) genügt es zu zeigen, dass die
Zufallsvariablen
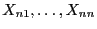 mit
mit
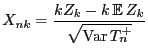 |
(24) |
den Bedingungen von Lemma 6.2 genügen.
- Dabei ergibt sich das Erfülltsein von (19)
unmittelbar aus der Definitionsgleichung (24).
- Es muss also lediglich noch gezeigt werden, dass die
Lindeberg-Bedingung (22) erfüllt ist.
- Mit Hilfe von Lemma 6.1 ergibt sich für die
Verteilungsfunktion
![$ F_{nk}:\mathbb{R}\to[0,1]$](img2555.png) der in
(24) eingeführten Zufallsvariablen
der in
(24) eingeführten Zufallsvariablen 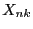 , dass
, dass
- Beachte
-




Nächste Seite: Zweistichproben-Probleme
Aufwärts: Vorzeichenrangtest von Wilcoxon
Vorherige Seite: Verteilung der Teststatistik für
Inhalt
Hendrik Schmidt
2006-02-27
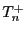 beruht auf der Darstellungsformel
(14).
beruht auf der Darstellungsformel
(14).
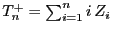 wegen Lemma 6.1 eine Summe von unabhängigen
Zufallsvariablen ist.
wegen Lemma 6.1 eine Summe von unabhängigen
Zufallsvariablen ist.
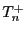 asymptotisch
normalverteilt ist.
asymptotisch
normalverteilt ist.
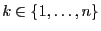
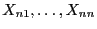 die in
(19) formulierten Bedingungen nicht erfüllen, dann
gehen wir zu den transformierten Zufallsvariablen
die in
(19) formulierten Bedingungen nicht erfüllen, dann
gehen wir zu den transformierten Zufallsvariablen
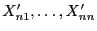 über mit
über mit
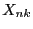 bezeichnen wir mit
bezeichnen wir mit 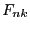 ,
wobei nicht ausgeschlossen wird, dass
,
wobei nicht ausgeschlossen wird, dass 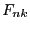 für jedes
für jedes
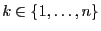 auch von der Anzahl
auch von der Anzahl  der insgesamt
betrachteten Zufallsvariablen
der insgesamt
betrachteten Zufallsvariablen
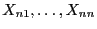 abhängen
kann.
abhängen
kann.