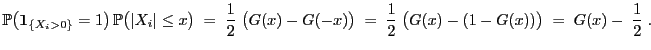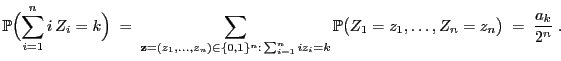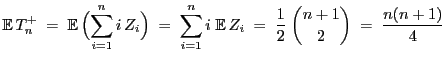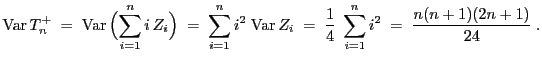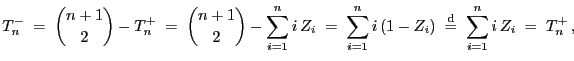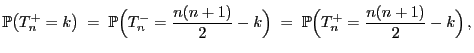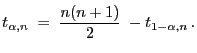Nächste Seite: Asymptotische Verteilung
Aufwärts: Vorzeichenrangtest von Wilcoxon
Vorherige Seite: Modellbeschreibung; Mediantest
Inhalt
Verteilung der Teststatistik 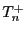 für kleine
Stichprobenumfänge
für kleine
Stichprobenumfänge
- Wenn der Stichprobenumfang
 nicht zu groß ist, dann lassen sich
die Quantile
nicht zu groß ist, dann lassen sich
die Quantile
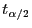 und
und
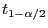 in
(13) durch kombinatorische Überlegungen bestimmen.
in
(13) durch kombinatorische Überlegungen bestimmen.
- Außerdem ist der folgende Hilfssatz nützlich, um die Verteilung
von
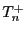 zu bestimmen.
zu bestimmen.
- Beweis
-
Theorem 6.3

Unter
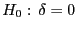
ist die Verteilung von
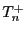
gegeben
durch
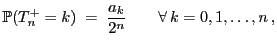 |
(15) |
wobei
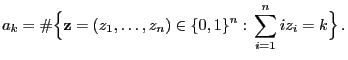 |
(16) |
Außerdem gilt dann
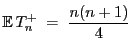 und und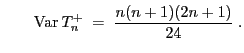 |
(17) |
- Beweis
-
- Aus der Darstellungsformel (14) für
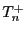 und aus
Lemma 6.1 ergibt sich, dass für jedes
und aus
Lemma 6.1 ergibt sich, dass für jedes
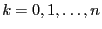
- Außerdem ergibt sich auf diese Weise, dass
und

- Beachte
-
- Aus (12) und (14) ergibt sich
darüber hinaus mit Hilfe von Lemma 6.1, dass
d.h., unter
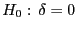 gilt
gilt
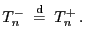 |
(18) |
- Somit ergibt sich aus (12), dass für jedes
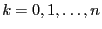 d.h., die Verteilung von
d.h., die Verteilung von 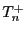 ist symmetrisch bezüglich des
Erwartungswertes
ist symmetrisch bezüglich des
Erwartungswertes
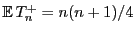 .
.
- Dies bedeutet, dass auch die Quantile
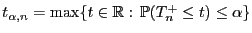 diese
Symmetrieeigenschaft besitzen, d.h., für jedes
diese
Symmetrieeigenschaft besitzen, d.h., für jedes
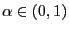 gilt
gilt
- Die Quantile
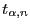 können entweder aus Tabellen
entnommen oder per Monte-Carlo-Simulation bestimmt werden.
können entweder aus Tabellen
entnommen oder per Monte-Carlo-Simulation bestimmt werden.




Nächste Seite: Asymptotische Verteilung
Aufwärts: Vorzeichenrangtest von Wilcoxon
Vorherige Seite: Modellbeschreibung; Mediantest
Inhalt
Hendrik Schmidt
2006-02-27