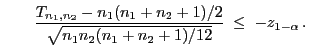Nächste Seite: Über dieses Dokument ...
Aufwärts: Zweistichproben-Probleme
Vorherige Seite: Iterationstest von Wald-Wolfowitz
Inhalt
Rangsummentest von Wilcoxon für Lagealternativen
- Wir diskutieren nun einen weiteren nichtparametrischen Test für
den Fall, dass zwei unabhängige Zufallsstichproben
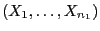 und
und
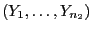 beobachtet
werden.
beobachtet
werden.
- Dabei werden jedoch jetzt speziellere Alternativen als in
(26) - (28) betrachtet.
- Genauso wie in Abschnitt 6.3.1 vereinigen wir die
Stichprobenvariablen
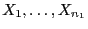 und
und
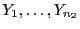 zu einer kombinierten Zufallsstichprobe
zu einer kombinierten Zufallsstichprobe
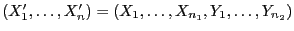 ,
wobei
,
wobei 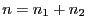 .
.
- Außerdem betrachten wir den (Zufalls-) Vektor der Ränge
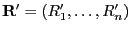 der
Stichprobenvariablen
der
Stichprobenvariablen
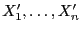 in der
kombinierten Stichprobe, wobei
in der
kombinierten Stichprobe, wobei
- So wie in Abschnitt 6.3.1 ist unter
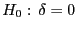 zu erwarten, dass die
zu erwarten, dass die 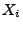 's und
's und 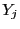 's in der kombinierten
Stichprobe
's in der kombinierten
Stichprobe
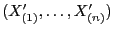 ,,gut
gemischt'' sind, weil dann die Stichprobenvariablen
,,gut
gemischt'' sind, weil dann die Stichprobenvariablen
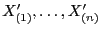 unabhängig und identisch
verteilt sind.
unabhängig und identisch
verteilt sind.
- Daher wird
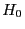 bei dem zweiseitigen Testproblem in
(30) abgelehnt, wenn die Rangsumme
bei dem zweiseitigen Testproblem in
(30) abgelehnt, wenn die Rangsumme
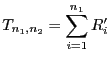 |
(32) |
,,zu klein'' oder ,,zu groß'' ist.
- Um den Test praktisch durchführen zu können, muss die Verteilung
der in (32) eingeführten Teststatistik
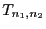 bestimmt werden. Hierfür ist der folgende Hilfssatz
nützlich.
bestimmt werden. Hierfür ist der folgende Hilfssatz
nützlich.
- Beweis
-
Theorem 6.5
- Unter
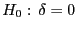 ist die Verteilung von
ist die Verteilung von
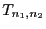 gegeben durch
gegeben durch
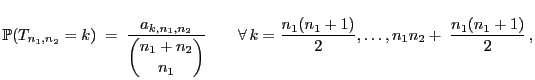 |
(34) |
wobei
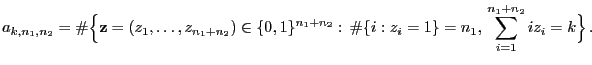 |
(35) |
- Außerdem gilt dann
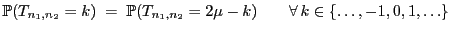 |
(36) |
und somit
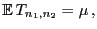 |
(37) |
wobei
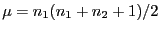 .
.
- Beweis
-
- Unter
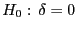 sind die Stichprobenvariablen
sind die Stichprobenvariablen
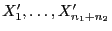 unabhängig und identisch
verteilt.
unabhängig und identisch
verteilt.
- Um (36) zu beweisen, nutzen wir die folgende
Symmetrieeigenschaft.
- Jedem
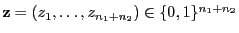 mit
mit
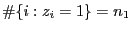
und
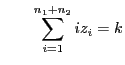
entspricht ein
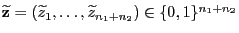 mit
mit
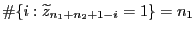
und
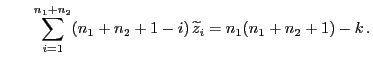
- Weil die Stichprobenvariablen
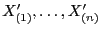 unabhängig und identisch
verteilt sind, ergibt sich somit, dass für jedes
unabhängig und identisch
verteilt sind, ergibt sich somit, dass für jedes
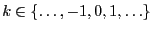
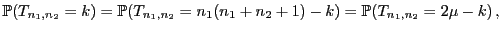 |
(38) |
wobei
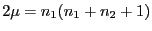 .
.
- Um (37) zu zeigen, genügt es in (38)
die Substitution
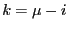 einzusetzen.
einzusetzen.
- Dann ergibt sich aus (38), dass
- Hieraus und aus Lemma 6.3 folgt die Gültigkeit von
(37).

- Beachte
-
Wenn die Stichprobenumfänge 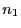 und
und 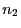 groß sind, dann ist
die direkte Bestimmung der Quantile
groß sind, dann ist
die direkte Bestimmung der Quantile
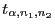 mit
Hilfe von Theorem 6.5 schwierig. Die
(näherungsweise) Bestimmung der Verteilung der Teststatistik
mit
Hilfe von Theorem 6.5 schwierig. Die
(näherungsweise) Bestimmung der Verteilung der Teststatistik
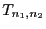 ist dann jedoch mit Hilfe des folgenden zentralen
Grenzwertsatzes, den wir hier ohne Beweis angeben.
ist dann jedoch mit Hilfe des folgenden zentralen
Grenzwertsatzes, den wir hier ohne Beweis angeben.
Theorem 6.6

Wenn
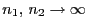
, so
dass
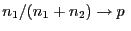
bzw.
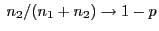
für ein
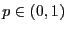
, dann gilt
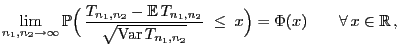 |
(39) |
wobei
und
![$ \Phi:\mathbb{R}\to[0,1]$](img2087.png)
die Verteilungsfunktion der
N
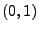
-Verteilung ist.
- Beachte
-




Nächste Seite: Über dieses Dokument ...
Aufwärts: Zweistichproben-Probleme
Vorherige Seite: Iterationstest von Wald-Wolfowitz
Inhalt
Hendrik Schmidt
2006-02-27
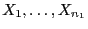 und
und
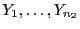 vollständig unabhängig sind mit den
(unbekannten) stetigen Verteilungsfunktionen
vollständig unabhängig sind mit den
(unbekannten) stetigen Verteilungsfunktionen 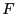 bzw.
bzw. 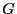 .
.
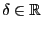 gibt, so dass
gibt, so dass
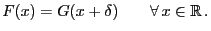
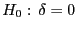 können die
folgenden Hypothesen betrachtet werden:
können die
folgenden Hypothesen betrachtet werden:
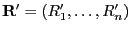 der
Stichprobenvariablen
der
Stichprobenvariablen
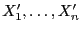 in der
kombinierten Stichprobe, wobei
in der
kombinierten Stichprobe, wobei
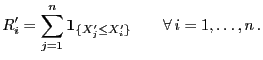
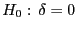 zu erwarten, dass die
zu erwarten, dass die 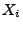 's und
's und 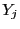 's in der kombinierten
Stichprobe
's in der kombinierten
Stichprobe
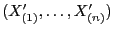 ,,gut
gemischt'' sind, weil dann die Stichprobenvariablen
,,gut
gemischt'' sind, weil dann die Stichprobenvariablen
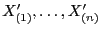 unabhängig und identisch
verteilt sind.
unabhängig und identisch
verteilt sind.
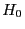 bei dem zweiseitigen Testproblem in
(30) abgelehnt, wenn die Rangsumme
bei dem zweiseitigen Testproblem in
(30) abgelehnt, wenn die Rangsumme
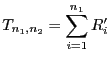
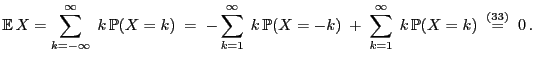
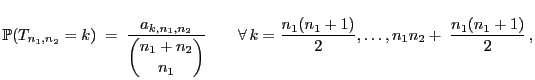
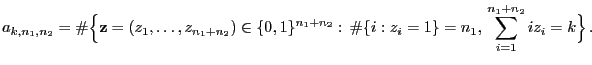
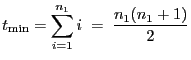 und
und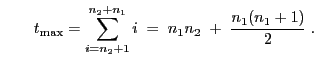
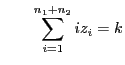
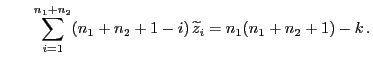
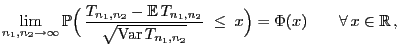
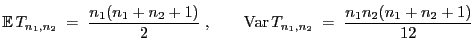
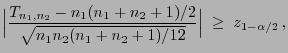
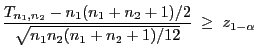 bzw.
bzw.