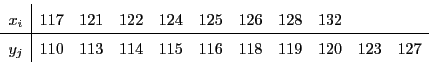Nächste Seite: Rangsummentest von Wilcoxon für
Aufwärts: Zweistichproben-Probleme
Vorherige Seite: Zweistichproben-Probleme
Inhalt
Iterationstest von
Wald-Wolfowitz
- Zur Untersuchung des in (26) gegebenen Testproblems
kann der Iterationstest auf Zufälligkeit angewendet werden, der in
Abschnitt 6.1.2 diskutiert worden ist.
- Hierfür vereinigen wir die Stichprobenvariablen
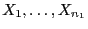 und
und
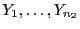 zu einer
Zufallsstichprobe
und betrachten die geordnete Stichprobe
zu einer
Zufallsstichprobe
und betrachten die geordnete Stichprobe
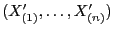 .
.
- Dabei setzen wir voraus, dass die Verteilungsfunktionen
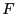 und
und
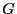 stetig sind, d.h., die Abbildung
ist mit Wahrscheinlichkeit
stetig sind, d.h., die Abbildung
ist mit Wahrscheinlichkeit 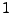 eindeutig festgelegt.
eindeutig festgelegt.
- Unter
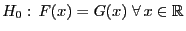 ist zu erwarten, dass
die
ist zu erwarten, dass
die 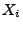 's und
's und 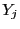 's in
's in
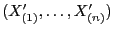 ,,gut gemischt'' sind,
,,gut gemischt'' sind,
- weil dann die Stichprobenvariablen
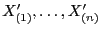 unabhängig und identisch
verteilt sind.
unabhängig und identisch
verteilt sind.
- Wenn als Alternative die Tendenz zur ,,Klumpen- bzw.
Clusterbildung'' betrachtet wird, dann wird
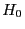 abgelehnt, wenn
die Anzahl
abgelehnt, wenn
die Anzahl 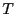 der Iterationen in der (binären) Stichprobe
der Iterationen in der (binären) Stichprobe
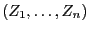 ,,zu klein'' ist, wobei
,,zu klein'' ist, wobei 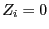 , wenn
, wenn
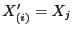 für ein
für ein
 , und
, und 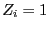 ,
wenn
,
wenn
 für ein
für ein
 .
.
- Beispiel
-
- Beachte
-
- Der in diesem Abschnitt betrachtete Iterationstest kann einseitige
Alternativen vom Typ (27) bzw.
(28) nicht erkennen.
- Dies wird durch das in (29) gegebene Beispiel klar:
Denn die Anzahl der Iterationen
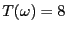 ändert sich nicht,
wenn wir (umgekehrt zu der bisherigen Vorgehensweise) den
Körpergrößen der Jungen jeweils eine
ändert sich nicht,
wenn wir (umgekehrt zu der bisherigen Vorgehensweise) den
Körpergrößen der Jungen jeweils eine 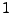 bzw. den Körpergrößen der
Mädchen jeweils eine 0 zuordnen.
bzw. den Körpergrößen der
Mädchen jeweils eine 0 zuordnen.
- Auch bei zweiseitigen Alternativen sollte der Iterationstest von
Wald-Wolfowitz, der ein so genannter ,,Omnibustest'' ist, nur
dann verwendet werden, wenn die Form der Alternative nicht näher
spezifiziert wird.
- Beim Vorliegen spezieller Alternativen, die beispielsweise nur
Lage- oder Variabilitätskenngrößen betreffen, sind andere
Testverfahren effizienter, vgl. Abschnitt 6.3.2.




Nächste Seite: Rangsummentest von Wilcoxon für
Aufwärts: Zweistichproben-Probleme
Vorherige Seite: Zweistichproben-Probleme
Inhalt
Hendrik Schmidt
2006-02-27
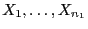 und
und
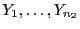 zu einer
Zufallsstichprobe
und betrachten die geordnete Stichprobe
zu einer
Zufallsstichprobe
und betrachten die geordnete Stichprobe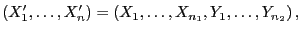
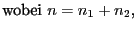

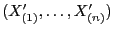 .
.
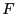 und
und
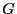 stetig sind, d.h., die Abbildung
ist mit Wahrscheinlichkeit
stetig sind, d.h., die Abbildung
ist mit Wahrscheinlichkeit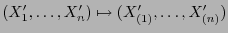
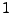 eindeutig festgelegt.
eindeutig festgelegt.
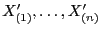 unabhängig und identisch
verteilt sind.
unabhängig und identisch
verteilt sind.
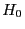 abgelehnt, wenn
die Anzahl
abgelehnt, wenn
die Anzahl 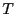 der Iterationen in der (binären) Stichprobe
der Iterationen in der (binären) Stichprobe
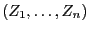 ,,zu klein'' ist, wobei
,,zu klein'' ist, wobei 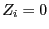 , wenn
, wenn
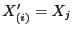 für ein
für ein
 , und
, und 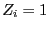 ,
wenn
,
wenn
 für ein
für ein
 .
.