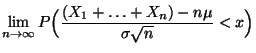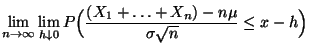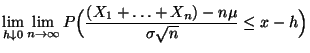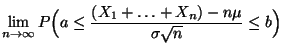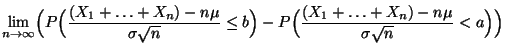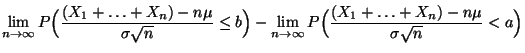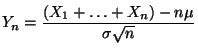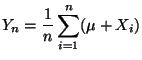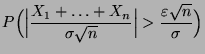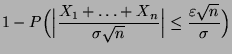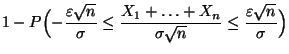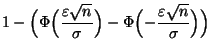Next: Methoden der Statistik
Up: Abschätzungen und Grenzwertsätze
Previous: Beispiel (Buffonsches Nadelexperiment)
Contents
Zentraler Grenzwertsatz
Neben der stochastischen Konvergenz und der fast sicheren
Konvergenz, die in Abschnitt 4.3.2 eingeführt wurden,
gibt es noch weitere Konvergenzarten von Zufallsvariablen.
Wir diskutieren nun
- den Begriff Konvergenz in Verteilung und in diesem Zusammenhang
- eine weitere Kategorie von Grenzwertsätzen, den sogenannten
zentralen Grenzwertsatz.
- Dabei wird eine andere Normierung der Summe
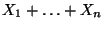 als
beim Gesetz der großen Zahlen betrachtet.
als
beim Gesetz der großen Zahlen betrachtet.
- Während die Normierung
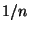 beim Gesetz der großen
Zahlen zu dem deterministischen Grenzwert
beim Gesetz der großen
Zahlen zu dem deterministischen Grenzwert 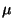 führt, wird nun die (kleinere) Normierung
führt, wird nun die (kleinere) Normierung
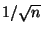 betrachtet, die zu einem nichtdeterministischen, d.h.
zufälligen Grenzwert führt.
betrachtet, die zu einem nichtdeterministischen, d.h.
zufälligen Grenzwert führt.
In Verallgemeinerung des zentralen Grenzwertsatzes von
DeMoivre-Laplace, der bereits in Abschnitt 3.2.3 erwähnt
wurde, gilt
- Theorem 4.24

 Sei
Sei
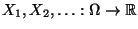 eine Folge von unabhängigen und identisch verteilten
Zufallsvariablen mit
eine Folge von unabhängigen und identisch verteilten
Zufallsvariablen mit
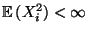 und
Var
und
Var 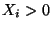 für alle
für alle
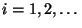 ;
;
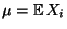 ,
,
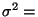 Var
Var  . Dann gilt für jedes
. Dann gilt für jedes
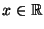
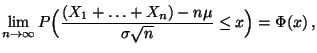 |
(48) |
wobei 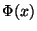 die Verteilungsfunktion der
Standardnormalverteilung ist.
die Verteilungsfunktion der
Standardnormalverteilung ist.
- Beweis
 Der Beweis von Theorem 4.24 ist tiefliegend und
geht über den Rahmen dieser einführenden Vorlesung hinaus.
Der Beweis von Theorem 4.24 ist tiefliegend und
geht über den Rahmen dieser einführenden Vorlesung hinaus.
- Korollar 4.25
- Unter den Voraussetzungen von Theorem 4.24
gilt
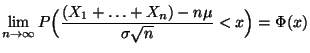 |
(49) |
für jedes
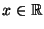 , und
, und
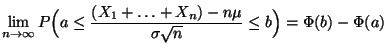 |
(50) |
für beliebige
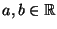 mit
mit 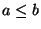 .
.
- Beweis
 Die Behauptung (49) ergibt sich
aus (48), weil
Die Behauptung (49) ergibt sich
aus (48), weil
Die Behauptung (50) ergibt sich nun
aus (48) und (49), denn es gilt
- Beachte
 Es ist die folgende Sprechweise üblich: Falls (48)
für jedes
Es ist die folgende Sprechweise üblich: Falls (48)
für jedes
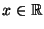 gilt, dann sagt man, daß
in Verteilung gegen die Standardnormalverteilung
(bzw. gegen eine N
gilt, dann sagt man, daß
in Verteilung gegen die Standardnormalverteilung
(bzw. gegen eine N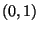 -verteilte Zufallsvariable
-verteilte Zufallsvariable
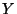 ) strebt.
) strebt.
Allgemein definiert man den Begriff der Verteilungskonvergenz von
Zufallsvariablen wie folgt.
- Definition 4.26
 Sei
Sei
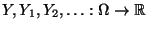 eine
beliebige Folge von Zufallsvariablen. Man sagt, daß die Zufallsvariablen
eine
beliebige Folge von Zufallsvariablen. Man sagt, daß die Zufallsvariablen
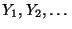 in Verteilung
gegen die Zufallsvariable
in Verteilung
gegen die Zufallsvariable 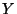 konvergieren, falls
konvergieren, falls
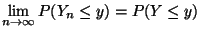 |
(51) |
für jedes
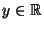 gilt, das ein Stetigkeitspunkt
der Verteilungsfunktion
gilt, das ein Stetigkeitspunkt
der Verteilungsfunktion 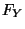 ist, d.h.
ist, d.h.
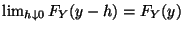 .
.
 Schreibweise:
Schreibweise:
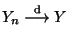
- Beachte
-
- Die Formel (51) ist offenbar gleichbedeutend mit
für jeden Stetigkeitspunkt
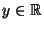 der Verteilungsfunktion
der Verteilungsfunktion
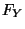 .
.
- Man kann darüber hinaus zeigen, daß
dies wiederum gleichbedeutend ist mit
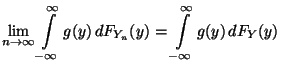 |
(52) |
für jede beschränkte und stetige Funktion
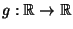 , wobei die Integrale in (52)
sogenannte Stieltjes-Integrale sind.
, wobei die Integrale in (52)
sogenannte Stieltjes-Integrale sind.
- In diesem Zusammenhang spricht man auch von der
schwachen Konvergenz der Verteilung von
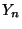 gegen die
Verteilung von
gegen die
Verteilung von 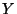 .
.
- Beispiel
 (fehlerbehaftete Messungen)
(fehlerbehaftete Messungen)




Next: Methoden der Statistik
Up: Abschätzungen und Grenzwertsätze
Previous: Beispiel (Buffonsches Nadelexperiment)
Contents
Roland Maier
2001-08-20