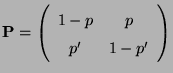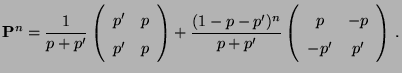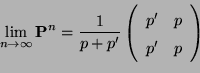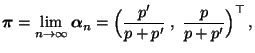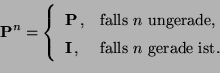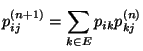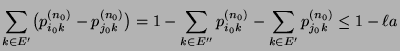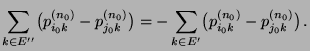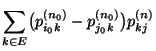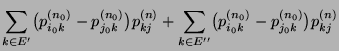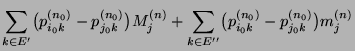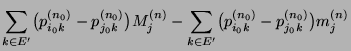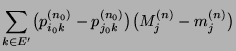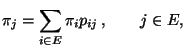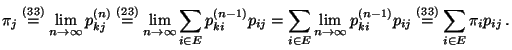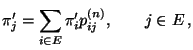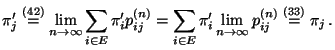Nächste Seite: Abschätzung der Konvergenzgeschwindigkeit; Perron-Frobenius-Theorem
Aufwärts: Ergodizität und Stationarität
Vorherige Seite: Ergodizität und Stationarität
Inhalt
Grundlegende Definitionen und quasi-positive
Übergangsmatrizen
- Wenn die Anzahl
 der potentiell möglichen Zustände der
Markov-Kette
der potentiell möglichen Zustände der
Markov-Kette
 sehr groß ist, dann ist die in
Abschnitt 2.1.4 diskutierte Spektraldarstellung
(30) der
sehr groß ist, dann ist die in
Abschnitt 2.1.4 diskutierte Spektraldarstellung
(30) der  -stufigen Übergangsmatrix
-stufigen Übergangsmatrix
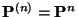 kein geeignetes Hilfsmittel, um
kein geeignetes Hilfsmittel, um
- die bedingten (Einzel-) Wahrscheinlichkeiten
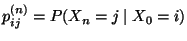 des zufälligen Zustandes
des zufälligen Zustandes 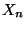
- bzw. die (unbedingten) Wahrscheinlichkeiten
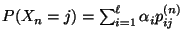 von
von 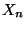
nach 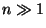 (Zeit-) Schritten zu berechnen.
(Zeit-) Schritten zu berechnen.
- Man kann jedoch Bedingungen angeben,
- unter denen die Grenzwerte
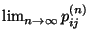 bzw.
bzw.
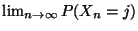 existieren (gleich sind und nicht von
existieren (gleich sind und nicht von
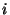 abhängen),
abhängen),
- so dass anstelle von
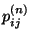 bzw.
bzw. 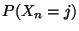 der Grenzwert
der Grenzwert
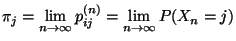 als Näherungslösung berechnet werden kann, falls
als Näherungslösung berechnet werden kann, falls 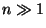 .
.
Dies führt zu dem folgenden Begriff der Ergodizität
von Markov-Ketten.
- Definition
 Die Markov-Kette
Die Markov-Kette
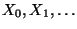 mit der Übergangsmatrix
mit der Übergangsmatrix
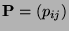 bzw. den zugehörigen
bzw. den zugehörigen 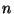 -stufigen
Übergangsmatrizen
-stufigen
Übergangsmatrizen
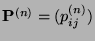
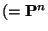 ) heißt
ergodisch, falls die Grenzwerte
) heißt
ergodisch, falls die Grenzwerte
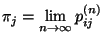 |
(33) |
- für jedes
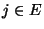 existieren,
existieren,
- positiv sind und nicht von
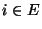 abhängen,
abhängen,
- eine Wahrscheinlichkeitsfunktion
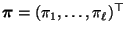 bilden, d.h.,
bilden, d.h.,
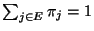 .
.
- Beispiel
 (Wettervorhersage)
(Wettervorhersage)
- Um den Begriff der Ergodizität von Markov-Ketten zu verdeutlichen,
kehren wir zunächst zu dem einfachen Beispiel der Wettervorhersage
zurück, das bereits in den Abschnitten 2.1.2 und
2.1.4 diskutiert wurde.
- Sei also
 , und sei
eine beliebige Übergangsmatrix mit
, und sei
eine beliebige Übergangsmatrix mit
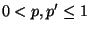 .
.
- Die
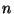 -stufige Übergangsmatrix
-stufige Übergangsmatrix
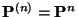 ist gegeben
durch
ist gegeben
durch
- Falls
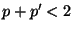 , dann ergibt sich hieraus und aus
(26), dass
bzw.
, dann ergibt sich hieraus und aus
(26), dass
bzw.
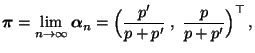 |
(34) |
wobei die Grenzverteilung
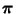 in (34) nicht von der Wahl der Anfangsverteilung
in (34) nicht von der Wahl der Anfangsverteilung
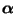
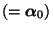 abhängt.
abhängt.
- Wenn jedoch
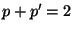 , dann gilt
, dann gilt
Die Ergodizität von Markov-Ketten mit allgemeinem (endlichen)
Zustandsraum lässt sich mit Hilfe des folgenden Begriffes aus der
Theorie positiver Matrizen charakterisieren.
- Definition
-
- Die
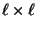 Matrix
Matrix
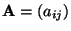 heißt nichtnegativ, falls sämtliche Eintragungen
heißt nichtnegativ, falls sämtliche Eintragungen 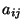 von
von
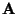 nichtnegativ sind.
nichtnegativ sind.
- Die nichtnegative Matrix
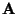 heißt quasi-positiv, falls
es eine natürliche Zahl
heißt quasi-positiv, falls
es eine natürliche Zahl 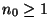 gibt, so dass sämtliche
Eintragungen von
gibt, so dass sämtliche
Eintragungen von
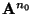 positiv sind.
positiv sind.
- Beachte
-
Falls
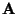 eine stochastische Matrix ist,
für die es eine natürliche Zahl
eine stochastische Matrix ist,
für die es eine natürliche Zahl 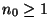 gibt, so dass sämtliche
Eintragungen von
gibt, so dass sämtliche
Eintragungen von
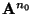 positiv sind, dann sind auch
sämtliche Eintragungen von
positiv sind, dann sind auch
sämtliche Eintragungen von
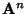 für jede natürliche
Zahl
für jede natürliche
Zahl 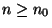 positiv.
positiv.
Theorem 2.4
Die Markov-Kette
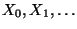
mit dem Zustandsraum
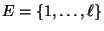
und der Übergangsmatrix

ist genau
dann ergodisch, wenn

quasi-positiv ist.
- Beweis
-
- Wir zeigen zunächst, dass die Bedingung
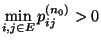 |
(35) |
für ein
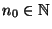 hinreichend für die Ergodizität von
hinreichend für die Ergodizität von 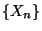 ist.
ist.
- Sei
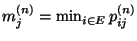 und
und
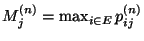 . Aus der
Chapman-Kolmogorov-Gleichung (23) ergibt sich dann,
dass
und somit
d.h.,
. Aus der
Chapman-Kolmogorov-Gleichung (23) ergibt sich dann,
dass
und somit
d.h.,
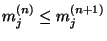 für jedes
für jedes 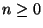 , wobei wir
, wobei wir
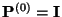 setzen. Auf die gleiche Weise ergibt sich,
dass
setzen. Auf die gleiche Weise ergibt sich,
dass
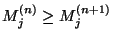 für jedes
für jedes 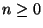 gilt.
gilt.
- Um die Existenz der Grenzwerte
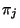 in (33) zu
beweisen, genügt es also zu zeigen, dass für jedes
in (33) zu
beweisen, genügt es also zu zeigen, dass für jedes 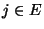
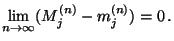 |
(36) |
- Hierfür betrachten wir für beliebige, jedoch fest vorgegebene
Zustände
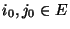 die Mengen
die Mengen
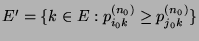 und
und
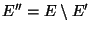 .
.
- Sei
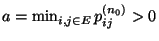 . Dann gilt
und
. Dann gilt
und
- Durch die erneute Anwendung der Chapman-Kolmogorov-Gleichung
(23) ergibt sich hieraus, dass für beliebige
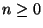 und
und 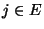
- Hieraus folgt, dass
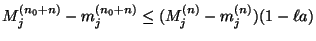 und (mit vollständiger Induktion) dass für jedes
und (mit vollständiger Induktion) dass für jedes 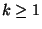
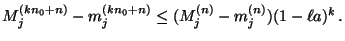 |
(37) |
- Es gibt also eine (unbegrenzt wachsende) Folge
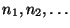 von natürlichen Zahlen, so dass für jedes
von natürlichen Zahlen, so dass für jedes 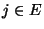
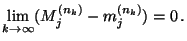 |
(38) |
- Weil die Differenzen
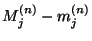 monoton in
monoton in 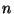 sind,
gilt (38) für jede (unbegrenzt wachsende)
Folge
sind,
gilt (38) für jede (unbegrenzt wachsende)
Folge
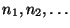 von natürlichen Zahlen.
von natürlichen Zahlen.
- Damit ist die Gültigkeit von (36) bewiesen.
- Die Grenzwerte
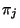 sind positiv, weil
sind positiv, weil
- Außerdem gilt
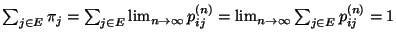 , weil die Vertauschung von Grenzwert und endlicher Summation erlaubt ist.
, weil die Vertauschung von Grenzwert und endlicher Summation erlaubt ist.
- Die Notwendigkeit der Bedingung (35) ergibt sich
unmitttelbar aus
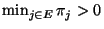 und (33),
wenn dabei berücksichtigt wird, dass der Zustandsraum
und (33),
wenn dabei berücksichtigt wird, dass der Zustandsraum  endlich
ist.
endlich
ist.

- Beachte
-
- Weil die Grenzwerte
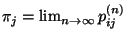 ergodischer Markov-Ketten nicht von
ergodischer Markov-Ketten nicht von 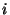 abhängen, ergibt sich
hieraus und aus der Endlichkeit des Zustandsraumes
abhängen, ergibt sich
hieraus und aus der Endlichkeit des Zustandsraumes
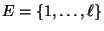 , dass
, dass
- Im Beweis von Theorem 2.4 wurde nicht nur die
Existenz der Grenzwerte
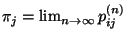 gezeigt, sondern die folgende Abschätzung der
Konvergenzgeschwindigkeit hergeleitet: Aus (37) ergibt
sich nämlich, dass
gezeigt, sondern die folgende Abschätzung der
Konvergenzgeschwindigkeit hergeleitet: Aus (37) ergibt
sich nämlich, dass
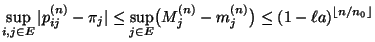 |
(39) |
bzw.
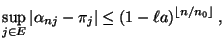 |
(40) |
wobei
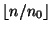 den ganzzahligen Teil von
den ganzzahligen Teil von
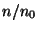 bezeichnet.
bezeichnet.
- Im Zusammenhang mit (39) und (40)
spricht man in der Literatur von geometrischen Schranken der
Konvergenzgeschwindigkeit.
Wir zeigen nun noch, dass die Grenzwerte
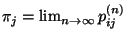 auch als Lösung eines linearen Gleichungssystems
aufgefasst werden können.
auch als Lösung eines linearen Gleichungssystems
aufgefasst werden können.
- Beweis
-
- Aus der Definitionsgleichung (33) der Grenzwerte
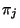 und aus der Chapman-Kolmogorov-Gleichung
(23) ergibt sich durch Vertauschen von Grenzwert
und Summation, dass
und aus der Chapman-Kolmogorov-Gleichung
(23) ergibt sich durch Vertauschen von Grenzwert
und Summation, dass
- Wir nehmen nun an, dass es noch eine weitere positive Lösung
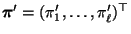 von
(41) gibt, so dass
von
(41) gibt, so dass
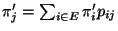 für jedes
für jedes 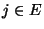 und
und
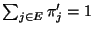 .
.
- Mit vollständiger Induktion kann man dann zeigen, dass
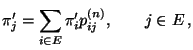 |
(42) |
für jedes
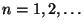 .
.
- Insbesondere ergibt sich somit aus (42), dass

- Beachte
-
- In Matrix-Schreibweise hat das lineare Gleichungssystem
(41) die Form
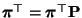 .
.
- Wenn die Anzahl
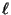 der Zustände nicht zu groß ist, dann kann
dieses Gleichungssystem ein Ausgangspunkt zur numerischen
Bestimmung der Wahrscheinlichkeitsfunktion
der Zustände nicht zu groß ist, dann kann
dieses Gleichungssystem ein Ausgangspunkt zur numerischen
Bestimmung der Wahrscheinlichkeitsfunktion
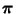 sein; vgl.
Abschnitt 2.2.5.
sein; vgl.
Abschnitt 2.2.5.
- Falls
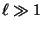 , dann ist in vielen Fällen dynamische
Monte-Carlo-Simulation besser zur Bestimmnug von
, dann ist in vielen Fällen dynamische
Monte-Carlo-Simulation besser zur Bestimmnug von
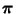 geeignet; vgl. Abschnitt 3.3.
geeignet; vgl. Abschnitt 3.3.




Nächste Seite: Abschätzung der Konvergenzgeschwindigkeit; Perron-Frobenius-Theorem
Aufwärts: Ergodizität und Stationarität
Vorherige Seite: Ergodizität und Stationarität
Inhalt
Ursa Pantle
2003-09-29
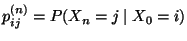 des zufälligen Zustandes
des zufälligen Zustandes 
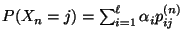 von
von 
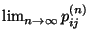 bzw.
bzw.
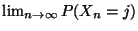 existieren (gleich sind und nicht von
existieren (gleich sind und nicht von
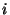 abhängen),
abhängen),
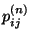 bzw.
bzw. 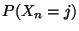 der Grenzwert
der Grenzwert
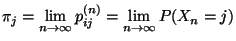 als Näherungslösung berechnet werden kann, falls
als Näherungslösung berechnet werden kann, falls 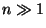 .
.