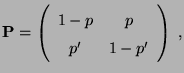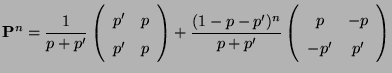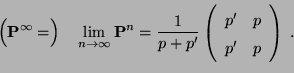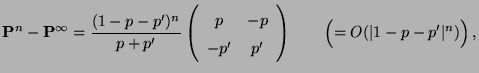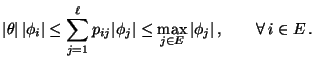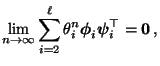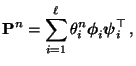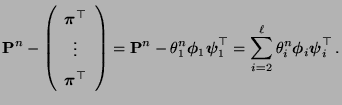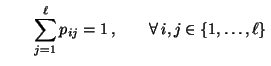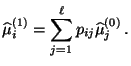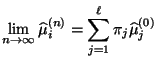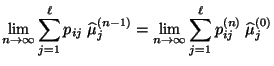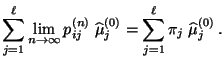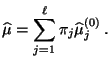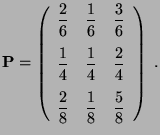Nächste Seite: Irreduzibilität und Aperiodizität
Aufwärts: Ergodizität und Stationarität
Vorherige Seite: Grundlegende Definitionen und quasi-positive
Inhalt
Abschätzung der Konvergenzgeschwindigkeit;
Perron-Frobenius-Theorem
- Zur Erinnerung
- Wenn das Minimum
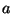 der Eintragungen
der Eintragungen 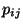 der Übergangsmatrix
der Übergangsmatrix
 nahe bei 0 liegt, dann ist die Schranke in
(43) nur von geringem Nutzen.
nahe bei 0 liegt, dann ist die Schranke in
(43) nur von geringem Nutzen.
- In manchen Fällen lässt sich jedoch die ,,Basis''
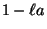 der
Konvergenzabschätzung in (43) verbessern.
der
Konvergenzabschätzung in (43) verbessern.
- Beispiel
 (Wettervorhersage)
(Wettervorhersage)
- Sei
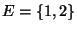 und
und
- In Abschnitt 2.2.1 hatten wir gezeigt,
- dass dann die
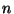 -stufige Übergangsmatrix
-stufige Übergangsmatrix
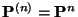 gegeben ist durch
gegeben ist durch
- und dass somit
- In diesem Fall ergibt sich also, dass
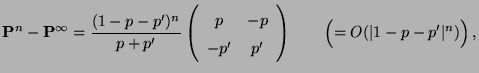 |
(44) |
wobei
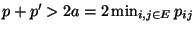 und somit
und somit
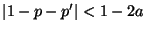 , falls
, falls
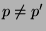 .
.
- Beachte
Im allgemeinen lassen sich geometrische Konvergenzabschätzungen
der Form (44) mit Hilfe des folgenden Theorems
von Perron-Frobenius für quasi-positive Matrizen herleiten.
Theorem 2.6
- Sei
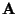 eine quasi-positive
eine quasi-positive
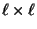 Matrix mit den
Eigenwerten
Matrix mit den
Eigenwerten
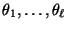 , so dass
, so dass
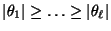 .
.
- Dann gilt:
- (a)
- Der Eigenwert
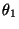 ist rellwertig und positiv,
ist rellwertig und positiv,
- (b)
-
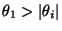 für jedes
für jedes
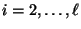 ,
,
- (c)
- die rechten bzw. linken (zu
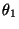 gehörenden) Eigenvektoren
gehörenden) Eigenvektoren
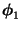 bzw.
bzw.
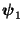 sind (bis auf einen konstanten
Faktor) eindeutig bestimmt und können so gewählt werden, dass
sämtliche Komponenten von
sind (bis auf einen konstanten
Faktor) eindeutig bestimmt und können so gewählt werden, dass
sämtliche Komponenten von
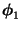 bzw.
bzw.
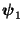 positiv
sind.
positiv
sind.
Einen Beweis von Theorem 2.6 kann man
beispielsweise in Kapitel 1 des Buches E. Seneta (1981) Non-Negative Matrices and Markov Chains, Springer-Verlag, New
York finden.
- Beweis
-
- Weil
 eine stochastische Matrix ist,
eine stochastische Matrix ist,
- gilt offenbar
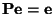 , und aus (41)
ergibt sich, dass
, und aus (41)
ergibt sich, dass
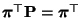 .
.
- Hieraus folgt, dass
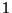 ein Eigenwert von
ein Eigenwert von
 ist und dass
ist und dass
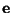 bzw.
bzw.
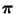 ein rechter bzw. linker Eigenvektor dieses
Eigenwertes ist.
ein rechter bzw. linker Eigenvektor dieses
Eigenwertes ist.
- Sei nun
- Aus Theorem 2.6 folgt nun, dass
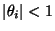 für
jedes
für
jedes
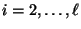 .
.

Aus Korollar 2.3 ergibt sich die folgende geometrische
Konvergenzabschätzung.
Korollar 2.4

Sei

eine quasi-positive Übergangsmatrix, so dass sämtliche
Eigenwerte
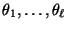
von

voneinander
verschieden sind. Dann gilt
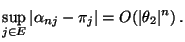 |
(45) |
- Beweis
-
- Beispiel
 (Konsensbildung)
(Konsensbildung)
vgl. C. Hesse (2003) Angewandte Wahrscheinlichkeitstheorie.
Vieweg-Verlag, Braunschweig, S. 349
- Eine Experten-Kommission, die aus
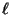 Mitgliedern besteht, soll
eine Prognose für einen (Wirtschafts-) Parameter
Mitgliedern besteht, soll
eine Prognose für einen (Wirtschafts-) Parameter
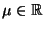 erstellen, beispielsweise der ,,Rat der Fünf Weisen'' eine
Prognose für das Wirtschaftswachstum im kommenden Jahr.
erstellen, beispielsweise der ,,Rat der Fünf Weisen'' eine
Prognose für das Wirtschaftswachstum im kommenden Jahr.
- Dabei entwickelt zunächst jeder der
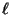 Experten eine eigene
Prognose für
Experten eine eigene
Prognose für 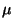 , wobei die einzelnen Prognosewerte mit
, wobei die einzelnen Prognosewerte mit
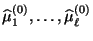 bezeichnet
werden und typischerweise voneinander verschieden sind.
bezeichnet
werden und typischerweise voneinander verschieden sind.
- Wie können nun die Experten hieraus eine gemeinsame Prognose
der gesamten Kommission, d.h., einen Konsens bilden?
- Eine einfache Vorgehensweise wäre die Bildung des arithmetischen
Mittels
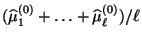 , wobei
jedoch die Kompetenzunterschiede zwischen den einzelnen Experten
unberücksicht bleiben würden.
, wobei
jedoch die Kompetenzunterschiede zwischen den einzelnen Experten
unberücksicht bleiben würden.
- Eine alternative Vorgehensweise besteht darin, dass jeder Experte
seine eigene Prognose nach Kenntnisnahme der Prognosen der anderen
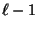 Experten und unter Berücksichtigung seiner Einschätzung
der prognostischen Fähigkeiten der Kommissionsmitglieder
modifiziert.
Experten und unter Berücksichtigung seiner Einschätzung
der prognostischen Fähigkeiten der Kommissionsmitglieder
modifiziert.
- Aus Theorem 2.4 folgt,
- Die Gültigkeit von (47) lässt sich dabei wie folgt
begründen. Es gilt nämlich
- Der Konsens der Experten-Kommission, d.h. die gemeinsame Prognose
des (unbekannten) Parameters
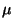 ist dann gegeben durch
ist dann gegeben durch
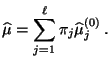 |
(48) |
- Beachte
-
- Für große
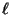 kann die direkte (algebraische) Lösung des
linearen Gleichungssystems (41) schwierig sein.
kann die direkte (algebraische) Lösung des
linearen Gleichungssystems (41) schwierig sein.
- Dann spielt die Abschätzung der Konvergenzgeschwindigkeit in
(47) eine wichtige Rolle bei der praktischen
Durchführung der in (47) beschriebenen
Konsensbildung.
- Wir betrachten hierfür das folgende Zahlenbeispiel.
- Sei
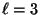 , und sei
, und sei
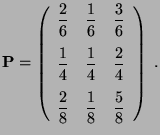 |
(49) |
- Die Eintragungen dieser stochastischen Matrix bedeuten, dass die
Kompetenz des dritten Experten von allen Kommissionsmitgliedern
besonders hoch eingeschätzt wird.
- Die Lösung
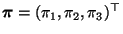 des entsprechenden
linearen Gleichungssystems (41) ist dann gegeben
durch
d.h., die Prognose
des entsprechenden
linearen Gleichungssystems (41) ist dann gegeben
durch
d.h., die Prognose
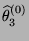 des dritten (als
besonders kompetent eingeschätzten) Experten wird am stärksten
gewichtet.
des dritten (als
besonders kompetent eingeschätzten) Experten wird am stärksten
gewichtet.
- Die Eigenwerte der in (49) gegebenen
Übergangsmatrix sind
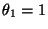 ,
,
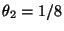 und
und
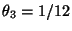 .
.
- Gemäß (43) ergibt sich dabei die ,,Basis''
der Konvergenzabschätzung, während Korollar 2.4 die
folgende (deutlich verbesserte) geometrische
Konvergenzabschätzung
liefert, wobei
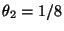 der zweitgrößte Eigenwert der in
(49) gegebenen stochastischen Matrix
der zweitgrößte Eigenwert der in
(49) gegebenen stochastischen Matrix
 ist,
vgl. auch Übungsaufgabe 3.3.
ist,
vgl. auch Übungsaufgabe 3.3.




Nächste Seite: Irreduzibilität und Aperiodizität
Aufwärts: Ergodizität und Stationarität
Vorherige Seite: Grundlegende Definitionen und quasi-positive
Inhalt
Ursa Pantle
2003-09-29
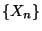 eine Markov-Kette ist, so dass
sämtliche Eintragungen
eine Markov-Kette ist, so dass
sämtliche Eintragungen 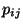 der (1-stufigen) Übergangsmatrix
der (1-stufigen) Übergangsmatrix
 positiv sind,
positiv sind,
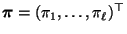 die folgende Form:
die folgende Form:
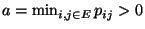 .
.