Nächste Seite: Schranken für die Eigenwerte
Aufwärts: Abschätzung der Konvergenzgeschwindigkeit; Reversibilität
Vorherige Seite: Alternative Abschätzung der Konvergenzgeschwindigkeit;
Inhalt
Dirichlet-Formen und Rayleigh-Theorem
- Sei
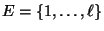 eine (beliebige) endliche Menge, und sei
eine (beliebige) endliche Menge, und sei
 eine
eine
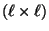 -dimensionale Übergangsmatrix, die
irreduzibel und aperiodisch (d.h. quasi-positiv) sowie reversibel
ist.
-dimensionale Übergangsmatrix, die
irreduzibel und aperiodisch (d.h. quasi-positiv) sowie reversibel
ist.
- Zur Erinnerung
- Sämtliche Eigenwerte von
 sind reell (vgl.
Abschnitt 2.3.3), und
sind reell (vgl.
Abschnitt 2.3.3), und
- aus dem Theorem von Perron-Frobenius (vgl.
Theorem 2.6 bzw. Korollar 2.3) folgt
darüber hinaus, dass die Eigenwerte von
 im Intervall
im Intervall
![$ (-1,1]$](img897.png) liegen,
liegen,
- wobei
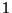 der größte Eigenwert ist, und die Beträge der anderen
Eigenwerte (strikt) kleiner als
der größte Eigenwert ist, und die Beträge der anderen
Eigenwerte (strikt) kleiner als 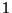 sind.
sind.
- Beachte
-
- In Abweichung von der bisher verwendeten Schreibweise (bei der die
Beträge der Eigenwerte betrachtet wurden) ordnen wir nun die
Eigenwerte selbst der Größe nach und bezeichnen sie mit
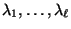 , so dass
, so dass
- Für die in Abschnitt 2.3.4 eingeführte multiplikativ
reversible Version
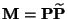 der
Übergangsmatrix
der
Übergangsmatrix
 gilt sogar
d.h., für die Eigenwerte der Matrix
gilt sogar
d.h., für die Eigenwerte der Matrix
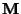 stimmen die beiden
Notationen
stimmen die beiden
Notationen
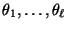 und
und
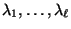 überein.
überein.
- Wenn
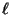 eine große Zahl ist,
eine große Zahl ist,
- dann kann die Berechnung des zweitgrößten Betrages
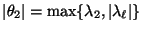 der Eigenwerte
schwierig sein,
der Eigenwerte
schwierig sein,
- weshalb wir in Abschnitt 2.3.7 Schranken für
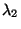 und
und
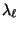 herleiten, deren Berechnung
einfacher ist.
herleiten, deren Berechnung
einfacher ist.
- Diese Schranken sind insbesondere dann nützlich, wenn
- die stationäre (Grenz-) Verteilung
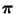 zwar (zumindest
prinzipiell) bekannt ist,
zwar (zumindest
prinzipiell) bekannt ist,
- die zugehörige Markov-Kette dennoch mit einer instationären
Anfangsverteilung
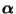 ,,gestartet'' wird, beispielsweise
in einem vorgegebenen Zustand
,,gestartet'' wird, beispielsweise
in einem vorgegebenen Zustand 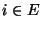 , wobei dann
, wobei dann
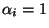 und
und
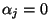 für
für 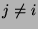 gilt.
gilt.
Um eine obere Schranke für 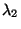 herzuleiten,
benötigen wir eine Darstellungsformel des Eigenwertes
herzuleiten,
benötigen wir eine Darstellungsformel des Eigenwertes 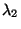 ,
,
Dabei zeigen wir zunächst den folgenden Hilfssatz.
- Beweis
 Aus der Definitionsgleichung (103) des
Skalarproduktes und aus der Reversibilität des Paares
Aus der Definitionsgleichung (103) des
Skalarproduktes und aus der Reversibilität des Paares
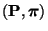 ergibt sich, dass
ergibt sich, dass

Wir beweisen nun das folgende Theorem von Rayleigh, das eine
Darstellungsformel für den zweitgrößten Eigenwert 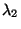 des
reversiblen Paares
des
reversiblen Paares
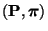 liefert.
liefert.
- Beweis
-
- Aus Lemma 2.8 ergibt sich, dass für beliebige
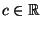 und
und
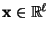
- Somit ist die Behauptung (117) äquivalent mit
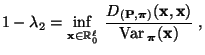 |
(118) |
wobei
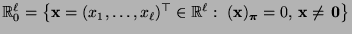 .
.
- Die rechten Eigenvektoren
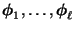 von
von
 seien nun so gewählt, dass sie eine orthonormale Basis in
seien nun so gewählt, dass sie eine orthonormale Basis in
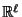 bezüglich des Skalarproduktes
bezüglich des Skalarproduktes
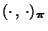 bilden, d.h., es gilt
bilden, d.h., es gilt
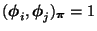 , falls
, falls 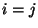 , und
, und
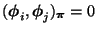 , falls
, falls 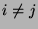 , wobei
, wobei
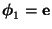 .
.
- Dabei werden zunächst die Eigenvektoren
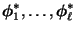 der symmetrischen Matrix
der symmetrischen Matrix
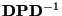 so gewählt, dass sie orthonormal
bezüglich des gewöhnlichen euklidischen Skalarproduktes sind,
wobei dann
so gewählt, dass sie orthonormal
bezüglich des gewöhnlichen euklidischen Skalarproduktes sind,
wobei dann
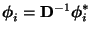 für jedes
für jedes 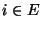 gesetzt wird (vgl. auch Abschnitt 2.3.3).
gesetzt wird (vgl. auch Abschnitt 2.3.3).
- Es gibt somit für jedes
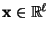 einen (eindeutig
bestimmten) Vektor
einen (eindeutig
bestimmten) Vektor
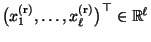 , so dass
, so dass
- Wegen
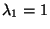 folgt hieraus, dass
folgt hieraus, dass
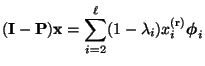
bzw.
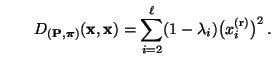
- Andererseits ergibt sich aus
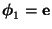 und aus der
Orthonormalität der Eigenvektoren
und aus der
Orthonormalität der Eigenvektoren
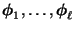 bezüglich des Skalarproduktes
bezüglich des Skalarproduktes
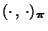 , dass
, dass




Nächste Seite: Schranken für die Eigenwerte
Aufwärts: Abschätzung der Konvergenzgeschwindigkeit; Reversibilität
Vorherige Seite: Alternative Abschätzung der Konvergenzgeschwindigkeit;
Inhalt
Ursa Pantle
2003-09-29
 sind reell (vgl.
Abschnitt 2.3.3), und
sind reell (vgl.
Abschnitt 2.3.3), und
 im Intervall
im Intervall
![$ (-1,1]$](img897.png) liegen,
liegen,
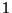 der größte Eigenwert ist, und die Beträge der anderen
Eigenwerte (strikt) kleiner als
der größte Eigenwert ist, und die Beträge der anderen
Eigenwerte (strikt) kleiner als 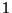 sind.
sind.
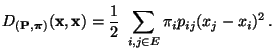
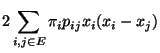
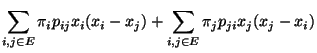
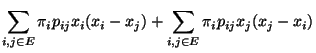
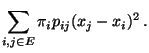
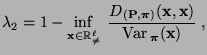
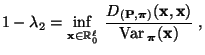
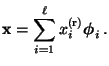
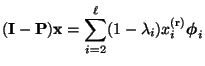 bzw.
bzw.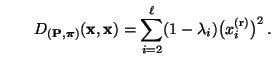
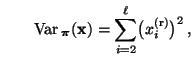 falls
falls