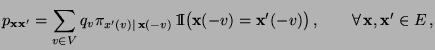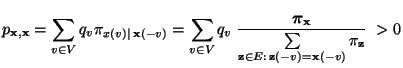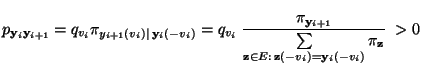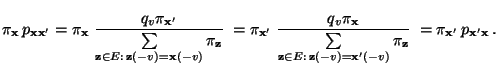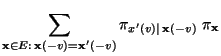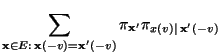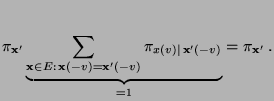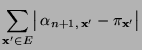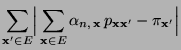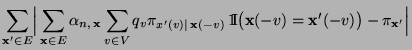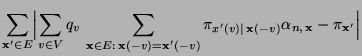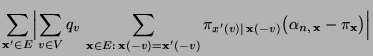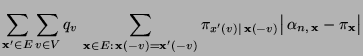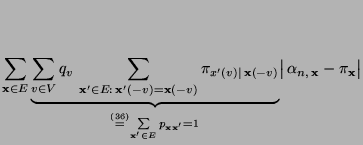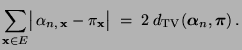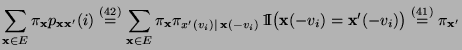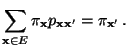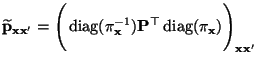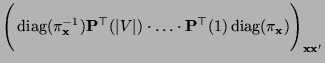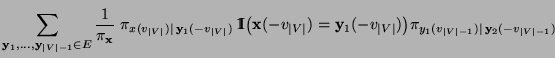Nächste Seite: Metropolis-Hastings-Algorithmus
Aufwärts: Simulationsmethoden mit Markov-Ketten
Vorherige Seite: Beispiel: Hard-Core-Modell
Inhalt
Gibbs-Sampler
Der in Abschnitt 3.3.1 betrachtete MCMC-Algorithmus,
um ,,zufällig ausgewählte'' zulässige Konfigurationen des
Hard-Core-Modells zu erzeugen, ist ein Spezialfall des
sogenannnten Gibbs-Samplers zur MCMC-Simulation von
diskreten (hochdimensionalen) Zufallsvektoren.
- MCMC-Simulationsalgorithmus
-
Theorem 3.11

Die Übergangsmatrix
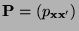
sei gegeben
durch
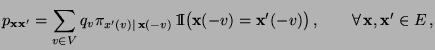 |
(36) |
wobei die bedingten Wahrscheinlichkeiten
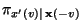
in
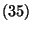
gegeben sind. Dann ist

irreduzibel und aperiodisch, und das Paar
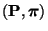
ist reversibel.
- Beweis
 Die Behauptung ergibt sich auf ähnliche Weise wie im Beweis von
Theorem 3.10.
Die Behauptung ergibt sich auf ähnliche Weise wie im Beweis von
Theorem 3.10.
- Um die Aperiodizität von
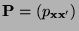 zu
zeigen, genügt es zu beachten,
zu
zeigen, genügt es zu beachten,
- dass für jedes
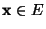
- und dass somit sämtliche Diagonalelemente
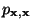 von
von
 positiv sind.
positiv sind.
- Die Irreduzibilität von
 ergibt sich aus den folgenden
Überlegungen.
ergibt sich aus den folgenden
Überlegungen.
- Es ist nun noch die Gültigkeit der Detailed-Balance-Gleichung
(2.85) zu zeigen, d.h., dass
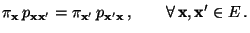 |
(38) |
Sei
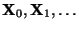 eine Markov-Kette mit dem
Zustandsraum
eine Markov-Kette mit dem
Zustandsraum 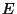 und mit der in (36) gegebenen
Übergangsmatrix
und mit der in (36) gegebenen
Übergangsmatrix
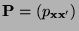 . Aus
Theorem 3.11 ergibt sich dann, dass
. Aus
Theorem 3.11 ergibt sich dann, dass
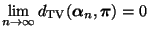 |
(39) |
für jede Anfangsverteilung
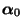 , wobei
, wobei
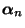 die
Verteilung von
die
Verteilung von
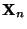 bezeichnet. Außerdem gilt für den
Gibbs-Sampler die folgende Monotonie-Eigenschaft.
bezeichnet. Außerdem gilt für den
Gibbs-Sampler die folgende Monotonie-Eigenschaft.
- Beweis
-
- Beachte
-
- Eine modifizierte Version des bisher in diesem Abschnitt
betrachteten Gibbs-Samplers ist der zyklische Gibbs-Sampler,
bei dem die jeweils zu aktualisierende Komponente
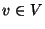
- nicht gemäß einer (vorgegebenen) Wahrscheinlichkeitsfunktion
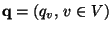 , so dass
, so dass 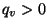 für jedes
für jedes 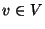 ,
ausgewählt wird,
,
ausgewählt wird,
- sondern die Komponenten
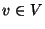 werden durchnumeriert und der
Reihe nach (auf deterministische Weise) ausgewählt.
werden durchnumeriert und der
Reihe nach (auf deterministische Weise) ausgewählt.
- Falls
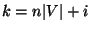 für gewisse Zahlen
für gewisse Zahlen
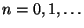 und
und
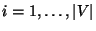 , dann ist die Matrix
, dann ist die Matrix
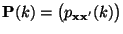 der
Übergangswahrscheinlichkeiten
der
Übergangswahrscheinlichkeiten
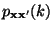 im
im
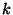 -ten Schritt gegeben durch
-ten Schritt gegeben durch
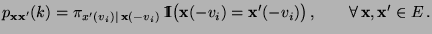 |
(42) |
- Für einen gesamten (Scan-) Zyklus, bei dem jede Komponente genau
einmal aktualisiert wird, ergibt sich die Übergangsmatrix
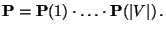 |
(43) |
- Man kann sich leicht überlegen, dass die in (42)
und (43) gegebene Matrix
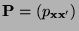
- irreduzibel und aperiodisch ist
- und dass
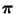 die stationäre (Grenz-) Verteilung von
die stationäre (Grenz-) Verteilung von
 ist,
ist,
- denn für jedes
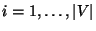 und für jedes
und für jedes
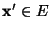 ergibt sich aus (41) und (42), dass
ergibt sich aus (41) und (42), dass
- und dass somit auch
- Das Paar
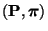 ist im allgemeinen nicht reversibel. In
Abschnitt 2.3.4 hatten wir jedoch gezeigt, dass das
Paar
ist im allgemeinen nicht reversibel. In
Abschnitt 2.3.4 hatten wir jedoch gezeigt, dass das
Paar
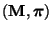 reversibel ist, wobei
reversibel ist, wobei
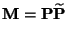 mit mit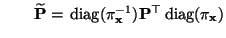 |
(44) |
die multiplikativ reversible Version von
 bezeichnet.
bezeichnet.
Theorem 3.13

Es gilt
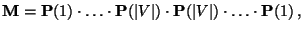 |
(45) |
d.h., die multiplikativ reversible Version
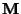
der
,,Vorwärts-Scan-Matrix''

stimmt mit der
,,Vorwärts-Rückwärts-Scan-Matrix'' überein.
- Beweis
-
- Beachte
-
- Bei der praktischen Anwendung von Gibbs-Samplern wird stets
vorausgesetzt,
- Dabei wird eine Familie
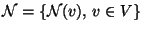 von
Teilmengen von
von
Teilmengen von 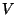 ein System von Nachbarschaften genannt,
falls für beliebige
ein System von Nachbarschaften genannt,
falls für beliebige 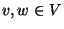
- (a)
-
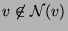 ,
,
- (b)
- aus
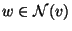 stets
stets
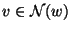 folgt.
folgt.
- Für das in Abschnitt 3.3.1 diskutierte Beispiel des
Hard-Core-Modells ist
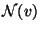 für jeden Eckpunkt
für jeden Eckpunkt 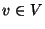 die
Menge derjenigen Eckpunkte
die
Menge derjenigen Eckpunkte 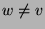 , die (direkt) mit
, die (direkt) mit 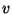 durch
eine Kante verbunden sind.
durch
eine Kante verbunden sind.




Nächste Seite: Metropolis-Hastings-Algorithmus
Aufwärts: Simulationsmethoden mit Markov-Ketten
Vorherige Seite: Beispiel: Hard-Core-Modell
Inhalt
Ursa Pantle
2003-09-29
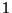 seine Werte in der endlichen
(Zustands-) Menge
seine Werte in der endlichen
(Zustands-) Menge
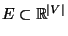 annimmt, wobei wir
voraussetzen,
annimmt, wobei wir
voraussetzen,
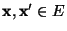 eine (endliche)
Folge von Zuständen
eine (endliche)
Folge von Zuständen
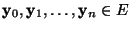 gibt, so
dass
gibt, so
dass
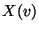 von
von
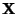 den Wert
den Wert 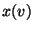 annimmt,
annimmt,
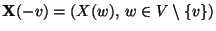 der übrigen Komponenten gleich
der übrigen Komponenten gleich
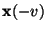 ist,
wobei vorausgesetzt wird, dass
ist,
wobei vorausgesetzt wird, dass
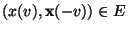 .
.