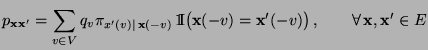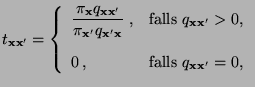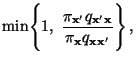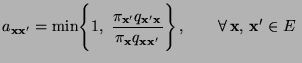- Der in (36) betrachtete Ansatz
für die Matrix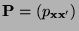 der
Übergangswahrscheinlichkeiten
der
Übergangswahrscheinlichkeiten
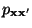 wird
verallgemeinert.
wird
verallgemeinert.
- Zusätzlich wird ein Verfahren zur Akzeptanz bzw. Verwerfung
der Updates
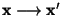 in den Algorithmus
integriert, dass auf einer ähnlichen Idee wie die in
Abschnitt 3.2.3 diskutierte Akzeptanz- und
Verwerfungsmethode beruht, vgl. insbesondere
Theorem 3.5.
in den Algorithmus
integriert, dass auf einer ähnlichen Idee wie die in
Abschnitt 3.2.3 diskutierte Akzeptanz- und
Verwerfungsmethode beruht, vgl. insbesondere
Theorem 3.5.
- der mit Wahrscheinlichkeit
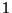 seine Werte in der endlichen
(Zustands-) Menge
seine Werte in der endlichen
(Zustands-) Menge
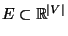 annimmt,
annimmt,
- wobei wir sowie bisher für die Wahrscheinlichkeitsfunktion
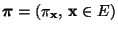 des Zufallsvektors
des Zufallsvektors
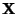 voraussetzen, dass
voraussetzen, dass
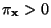 für jedes
für jedes
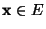 .
.
- wobei
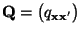 eine beliebige
stochastische Matrix ist, die irreduzibel und aperiodisch sei, so
dass
eine beliebige
stochastische Matrix ist, die irreduzibel und aperiodisch sei, so
dass
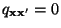 genau dann, wenn
genau dann, wenn
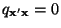 .
.
- die Matrix
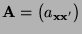 gegeben ist
durch
gegeben ist
durch
so dass
- und
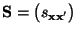 eine beliebige
symmetrische Matrix ist mit
eine beliebige
symmetrische Matrix ist mit