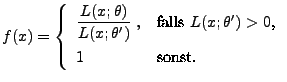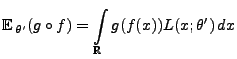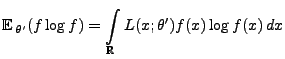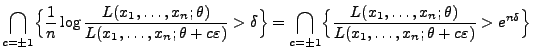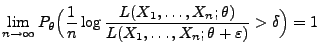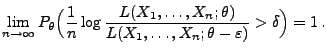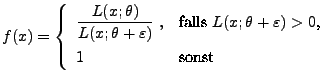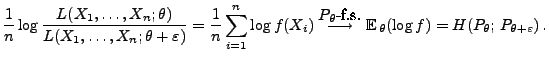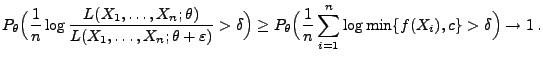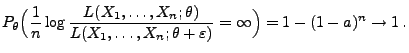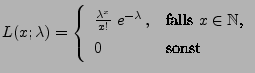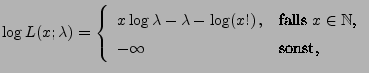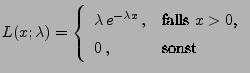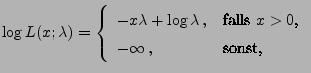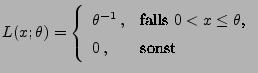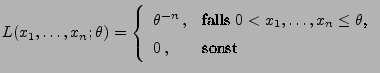- schwach konsistent, falls
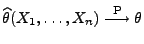 für jedes
für jedes
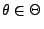 und für
und für
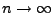 ,
d.h.,
,
d.h.,
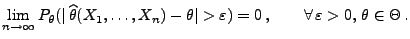
- stark konsistent, falls
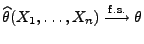 für jedes
für jedes
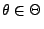 und für
und für
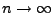 , d.h.,
, d.h.,
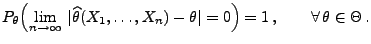
- Es gelte
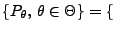 N
N
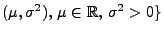 ,
wobei sowohl
,
wobei sowohl 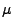 als auch
als auch 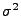 unbekannt sei.
unbekannt sei.
- Dann ergibt sich aus den Theoremen 1.2 bzw.
1.4, dass für
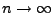
- Wegen der Erhaltung der (fast sicheren) Konvergenz bei Addition
bzw. Multiplikation (vgl. jeweils die Teilaussage 1 der
Theoreme WR-5.8 bzw. WR-5.10) ergibt sich aus
(57), dass für
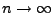
d.h., der (erwartungstreue) Schätzer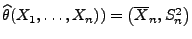 für
für
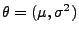 ist stark (und damit auch schwach)
konsistent.
ist stark (und damit auch schwach)
konsistent.
- Hieraus ergibt sich außerdem, dass auch der in Beispiel 5 des
Abschnittes 2.2.2 hergeleitete (asymptotisch
erwartungstreue) Maximum-Likelihood-Schätzer
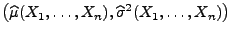 für
für
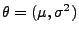 stark konsistent ist.
stark konsistent ist.
- Weil die Theoreme 1.2 und 1.4 nicht
nur für normalverteilte Stichprobenvariablen gelten, ist der
Schätzer
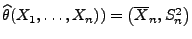 für jede parametrische Verteilungsfamile
konsistent, für die der Erwartungswert
für jede parametrische Verteilungsfamile
konsistent, für die der Erwartungswert 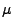 bzw. die Varianz
bzw. die Varianz
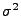 der Stichprobenvariablen zu den Komponenten des
Parametervektors
der Stichprobenvariablen zu den Komponenten des
Parametervektors 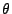 gehören.
gehören.
- Falls
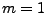 , dann kann man die folgende allgemeine Bedingung für
die schwache Konsistenz von (asymptotisch erwartungstreuen)
Schätzern formulieren.
, dann kann man die folgende allgemeine Bedingung für
die schwache Konsistenz von (asymptotisch erwartungstreuen)
Schätzern formulieren.
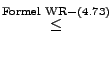
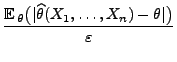

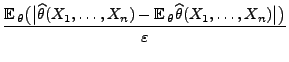
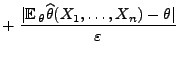

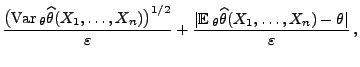

![$\displaystyle H(P_\theta;\,P_{\theta^\prime})=\left\{\begin{array}{ll}
\displa...
...(x;\theta^\prime)=0)=0$,}\\ [3\jot]
\infty &\mbox{sonst,}
\end{array}\right.$](img1441.png)