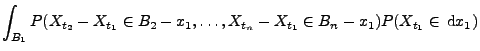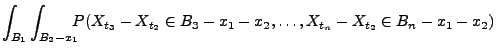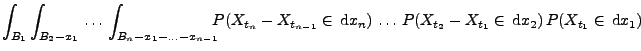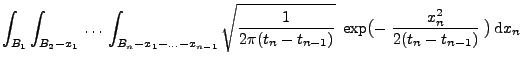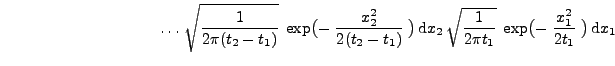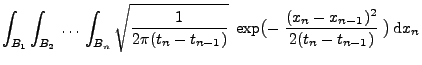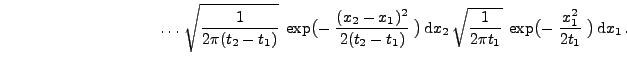Nächste Seite: Verteilung des Maximums
Aufwärts: Wiener-Prozess
Vorherige Seite: Konstruktion von Wiener-Prozessen; Simulationsalgorithmus
Inhalt
Darstellung als Markow-Prozess bzw. Gauß-Prozess
Wir zeigen nun, dass der Wiener-Prozess ein Markow-Prozess im
Sinne der folgenden (verallgemeinerten) Definition dieses
Begriffes ist, die ähnlich zu der in Abschnitt 2.3.1
betrachteten Definition von Markow-Prozessen mit endlichem
Zustandsraum ist.
Sei
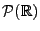 die Familie sämtlicher Wahrscheinlichkeitsmaße
auf der Borel-
die Familie sämtlicher Wahrscheinlichkeitsmaße
auf der Borel- -Algebra
-Algebra
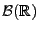 . Um den Begriff
eines Markow-Prozesses
. Um den Begriff
eines Markow-Prozesses
 mit stetiger Zeit und
mit Werten in dem (überabzählbaren) Zustandsraum
mit stetiger Zeit und
mit Werten in dem (überabzählbaren) Zustandsraum
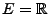 einzuführen, betrachten wir
einzuführen, betrachten wir
- ein Wahrscheinlichkeitsmaß
![$ {\boldsymbol{\alpha}}:\mathcal{B}(\mathbb{R})\to[0,1]$](img1112.png) sowie
sowie
- einen stochastischen Kern
![$ {\mathbf{P}}:\,[0,\infty)\times\mathbb{R}\times\mathcal{B}(\mathbb{R})\to[0,1]$](img1113.png) , so dass
, so dass
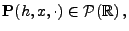 |
(15) |
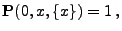 |
(16) |
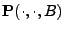  |
(17) |
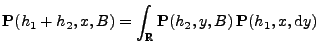 |
(18) |
für beliebige
 ,
,
 und
und
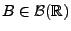 .
.
- Definition

- Ein stochastischer Kern
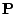 , der den Bedingungen
(15)-(18) genügt, wird Übergangskern genannt.
, der den Bedingungen
(15)-(18) genügt, wird Übergangskern genannt.
- Ein stochastischer Prozess
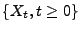 mit Werten in
mit Werten in
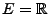 heißt homogener Markow-Prozess, wenn es einen Übergangskern
heißt homogener Markow-Prozess, wenn es einen Übergangskern
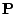 und ein Wahrscheinlichkeitsmaß
und ein Wahrscheinlichkeitsmaß
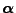 über
über
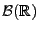 gibt, so dass
gibt, so dass
für beliebige
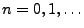 ,
,
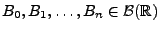 ,
,
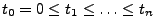 .
.
- Beachte

- Das Wahrscheinlichkeitsmaß
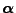 in (19) wird
Anfangsverteilung genannt.
in (19) wird
Anfangsverteilung genannt.
- Außerdem wird
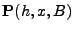 als die Wahrscheinlichkeit
interpretiert, dass der Prozess
als die Wahrscheinlichkeit
interpretiert, dass der Prozess  in
in 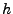 Zeiteinheiten vom
Zustand
Zeiteinheiten vom
Zustand 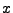 in einen Zustand aus
in einen Zustand aus 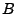 übergeht.
übergeht.
Theorem 2.22

Sei

ein Wiener-Prozess. Dann ist

ein
Markow-Prozess mit
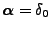
, d.h.,
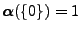
, und
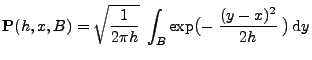 |
(20) |
für beliebige
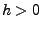
,
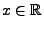
und
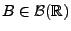
.
- Beweis
-
- Beachte
-




Nächste Seite: Verteilung des Maximums
Aufwärts: Wiener-Prozess
Vorherige Seite: Konstruktion von Wiener-Prozessen; Simulationsalgorithmus
Inhalt
Ursa Pantle
2005-07-13
![]() die Familie sämtlicher Wahrscheinlichkeitsmaße
auf der Borel-
die Familie sämtlicher Wahrscheinlichkeitsmaße
auf der Borel-![]() -Algebra
-Algebra
![]() . Um den Begriff
eines Markow-Prozesses
. Um den Begriff
eines Markow-Prozesses
![]() mit stetiger Zeit und
mit Werten in dem (überabzählbaren) Zustandsraum
mit stetiger Zeit und
mit Werten in dem (überabzählbaren) Zustandsraum
![]() einzuführen, betrachten wir
einzuführen, betrachten wir