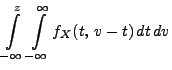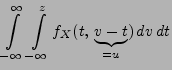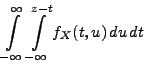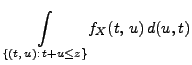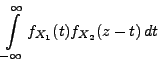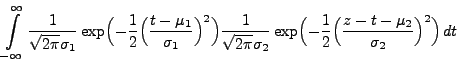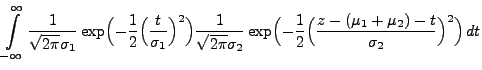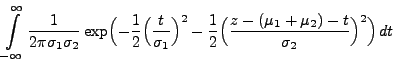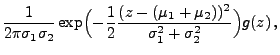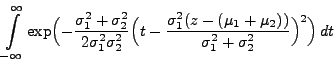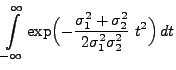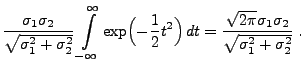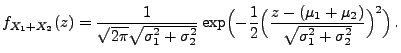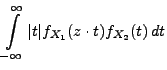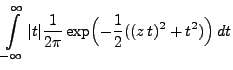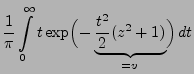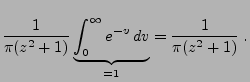Theorem 3.16
Sei
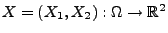
ein absolutstetiger Zufallsvektor mit der (gemeinsamen) Dichte
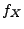
. Dann ist auch die Zufallsvariable
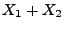
absolutstetig, und ihre Dichte ist gegeben durch
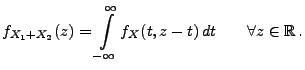 |
(44) |
Falls die Zufallsvariablen
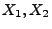
unabhängig sind, dann gilt
insbesondere die sogenannte
Faltungsformel
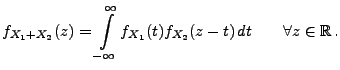 |
(45) |
Theorem 3.17
Die Zufallsvariablen
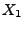
und
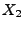
seien
unabhängig und absolutstetig mit den Dichten
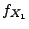
und
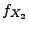
. Dann sind die Zufallsvariablen
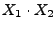
und
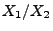
absolutstetig, und ihre
Dichten sind gegeben durch
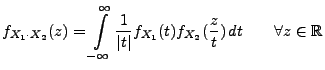 |
(47) |
bzw.
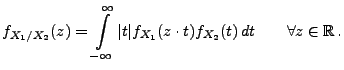 |
(48) |