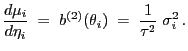Nächste Seite: Hesse-Matrix
Aufwärts: Maximum-Likelihood-Schätzer für
Vorherige Seite: Maximum-Likelihood-Schätzer für
Inhalt
Loglikelihood-Funktion und ihre partiellen Ableitungen
- Aus (2) - (3) bzw. aus
(11) ergibt sich, dass die Loglikelihood-Funktion
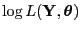 der Zufallsstichprobe
der Zufallsstichprobe
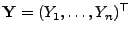 als eine Funktion
als eine Funktion
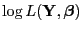 von
von
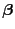 geschrieben werden kann.
geschrieben werden kann.
- Und zwar folgt aus (2) - (3),
dass
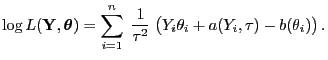 |
(23) |
- Hieraus und aus (11) ergibt sich nun, dass
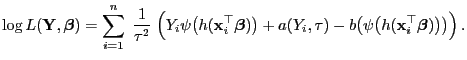 |
(24) |
- Für verallgemeinerte lineare Modelle mit natürlicher Linkfunktion
ergibt sich aus (13) und (23), dass
 |
(25) |
Zur Bestimmung von Maximum-Likelihood-Schätzern ist die Kenntnis
der so genannten Scorefunktionen, d.h. der partiellen Ableitungen
der Loglikelihood-Funktion, sowie der Fisher-Informationsmatrix
nützlich, die wie folgt definiert ist.
- Definition
 Für beliebige
Für beliebige
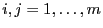 sei
sei
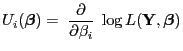
und
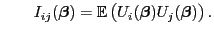
Dann wird der 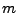 -dimensionale Zufallsvektor
-dimensionale Zufallsvektor
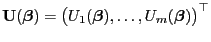 bzw. die (deterministische)
bzw. die (deterministische) 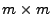 -Matrix
-Matrix
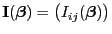 der Scorevektor bzw. die Fisher-Informationsmatrix genannt.
der Scorevektor bzw. die Fisher-Informationsmatrix genannt.
Mit der Schreibweise
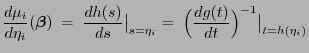 |
(26) |
ergibt sich das folgende Resultat.
Theorem 4.1

Für beliebige
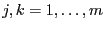
gilt
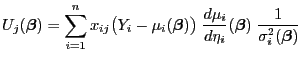 |
(27) |
und
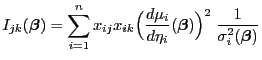 |
(28) |
bzw. in Matrix-Schreibweise
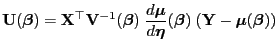 und und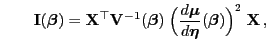 |
(29) |
wobei
- Beweis
-
- Die in (23) bzw. (24) gegebene
Loglikelihood-Funktion lässt sich in der Form
schreiben, wobei
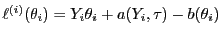 und
und
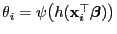 .
.
- Somit gilt für jedes
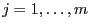 , dass
, dass
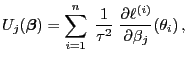 |
(30) |
wobei sich durch die mehrfache Anwendung der Kettenregel ergibt,
dass
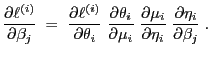 |
(31) |
- Andererseits gilt offenbar, dass
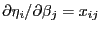 , und aus
Lemma 4.2 ergibt sich, dass
bzw.
, und aus
Lemma 4.2 ergibt sich, dass
bzw.
- Hieraus und aus (30) - (31)
ergibt sich die Gültigkeit von (27).
- Um (28) zu zeigen, genügt es zu beachten, dass für
beliebige
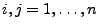 wegen der Unabhängigkeit der Stichprobenvariablen
wegen der Unabhängigkeit der Stichprobenvariablen
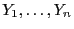 .
.
- Hieraus und aus (27) ergibt sich, dass
- Damit ist (28) bewiesen.

Korollar 4.1
Sei
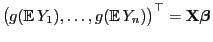
ein GLM mit natürlicher Linkfunktion
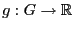
. Dann gilt für
beliebige
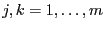
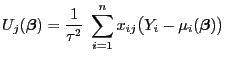 bzw. bzw.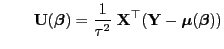 |
(32) |
und
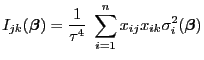 bzw. bzw.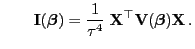 |
(33) |
- Beweis
 Weil
Weil
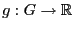 eine natürliche Linkfunktion ist, gilt
eine natürliche Linkfunktion ist, gilt
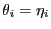 für jedes
für jedes
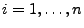 . Hieraus und aus
Lemma 4.2 ergibt sich, dass
Die Behauptung ergibt sich somit aus
Theorem 4.1.
. Hieraus und aus
Lemma 4.2 ergibt sich, dass
Die Behauptung ergibt sich somit aus
Theorem 4.1.





Nächste Seite: Hesse-Matrix
Aufwärts: Maximum-Likelihood-Schätzer für
Vorherige Seite: Maximum-Likelihood-Schätzer für
Inhalt
Hendrik Schmidt
2006-02-27
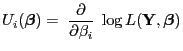 und
und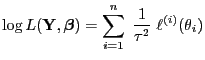
![$\displaystyle {\mathbb{E} }\bigl((Y_i-\mu_i)(Y_j-\mu_j)\bigr)=\left\{\begin{ar...
..._i^2 &\mbox{für $i=j$,} [3\jot]
0 &\mbox{für $i\not=j$.}
\end{array}\right.
$](img1672.png)