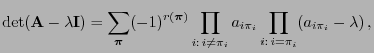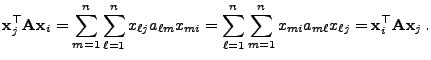heißt Eigenwert der Matrix
- Die Gleichung (2) hat nur für solche
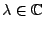 eine Lösung
eine Lösung
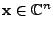 mit
mit
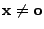 ,
für die
,
für die 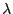 eine Lösung der so genannten charakteristischen Polynomgleichung
eine Lösung der so genannten charakteristischen Polynomgleichung
ist, wobei die linke Seite von (3) das charakteristische Polynom der
Matrix
von (3) das charakteristische Polynom der
Matrix
 genannt wird.
genannt wird.
- Seien
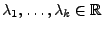 die reellwertigen
Lösungen von (3). Dann lässt sich das
charakteristische Polynom
die reellwertigen
Lösungen von (3). Dann lässt sich das
charakteristische Polynom
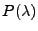 in der Form
in der Form
darstellen, wobei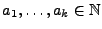 positive natürliche
Zahlen sind, genannt die algebraischen Vielfachheiten von
positive natürliche
Zahlen sind, genannt die algebraischen Vielfachheiten von
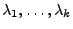 , und
, und
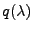 ein Polynom der
Ordnung
ein Polynom der
Ordnung
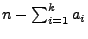 ist, das keine reellen Lösungen
besitzt.
ist, das keine reellen Lösungen
besitzt.