


Next: The Boolean Model
Up: Stationary Marked Point Processes
Previous: A Spatial Ergodic Theorem
In later sections of this paper we need Palm
distributions of a different kind than that given in (3.2). Roughly speaking,
such a (global) Palm distribution is the conditional distribution of
(X,M) under the condition that there are points of the
point process at a given set of locations. We begin with the simplest case
conditioning on the event that (X,M) has a point at a fixed location,
say at the origin.
Let A be a set of realizations of (X,M) and put
| 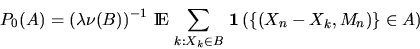 |
(4) |
where B is an arbitrary fixed Borel set with 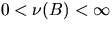 .By
.By 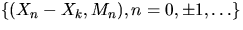 we denote the shifted point process which we obtain
after shifting all points of (X,M) by Xk. In particular, the point
Xk of (X,M) is shifted into the origin.
Clearly, the sum in (3.4) counts the shifted realizations lying in A.
Since we assume that (X,M) is stationary, the value P0(A) defined in
(3.4) does not depend on the choice of B. Moreover,
in many cases of practical interest we have
we denote the shifted point process which we obtain
after shifting all points of (X,M) by Xk. In particular, the point
Xk of (X,M) is shifted into the origin.
Clearly, the sum in (3.4) counts the shifted realizations lying in A.
Since we assume that (X,M) is stationary, the value P0(A) defined in
(3.4) does not depend on the choice of B. Moreover,
in many cases of practical interest we have
| 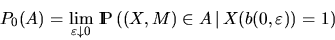 |
(5) |
which motivates the interpretation of P0 as conditional distribution of
(X,M) under the
condition that at the origin there is a point of the point process.
If (X,M) is ergodic and the sequence 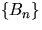 is an averaging sequence,
then analogous to (3.3)
is an averaging sequence,
then analogous to (3.3)
| 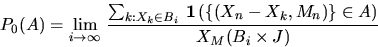 |
(6) |
which gives the motivation to say that P0(A) is the probability of
the event A, seen from the typical point of (X,M).
We remark that the notion of the Palm mark distribution
defined in (3.2) can be embedded into the more
general concept given by (3.4). Namely, if
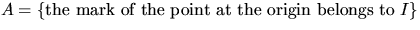 ,then
,then
because in this case
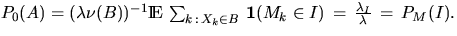
It is clear that a marked point process with distribution P0
is not stationary since, under P0, there is a point at the
origin with probability 1. However, if (X,M) is stationary
and isotropic, then a marked point process with distribution P0
is isotropic as well.
A further important notion is that of the reduced Palm distribution
P0! which is given by
| 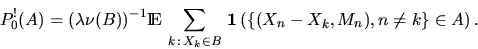 |
(8) |
This means that under P0!, the point at the origin is not counted.
Clearly, by omitting the marks in (3.4) and (3.8),
one can define the distributions P0 and P0! of an (unmarked)
stationary point process 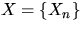 in the same way.
A famous result of the theory of stationary point processes is the
following theorem of Slivnyak: X is a Poisson process
if and only if
in the same way.
A famous result of the theory of stationary point processes is the
following theorem of Slivnyak: X is a Poisson process
if and only if
where P denotes the (unconditional) distribution of X. In other words,
the Palm distribution P0 of a homogeneous Poisson process is obtained
simply by adding a point at the origin. See e.g. Møller (1994)
for a proof of it.
Further details on Palm distributions of stationary marked point
processes on the plane and in higher-dimensional spaces can be found
e.g. in Daley and Vere-Jones (1988),
König and Schmidt (1992),
Møller (1994), Stoyan et al. (1995).
We also remark that their initial application was in queueing theory;
see e.g. Baccelli and Brémaud (1994),
Brandt et al. (1990), Franken et al. (1982).



Next: The Boolean Model
Up: Stationary Marked Point Processes
Previous: A Spatial Ergodic Theorem
Andreas Frey
7/8/1998
![]() is an averaging sequence,
then analogous to (3.3)
is an averaging sequence,
then analogous to (3.3)
![]() ,then
,then
![]() in the same way.
A famous result of the theory of stationary point processes is the
following theorem of Slivnyak: X is a Poisson process
if and only if
in the same way.
A famous result of the theory of stationary point processes is the
following theorem of Slivnyak: X is a Poisson process
if and only if