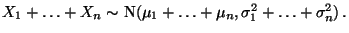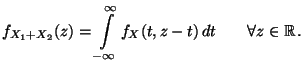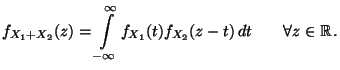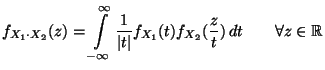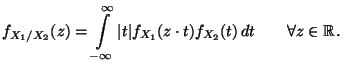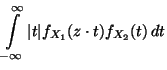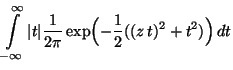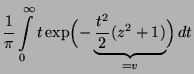Next: Weitere Charakteristiken von Zufallsvariablen;
Up: Funktionen von Zufallsvariablen
Previous: Quadrierung
Contents
Summe, Produkt und Quotient von unabhängigen
Zufallsvariablen
- Theorem 3.22
 Sei
Sei
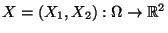 ein absolutstetiger Zufallsvektor mit der (gemeinsamen) Dichte
ein absolutstetiger Zufallsvektor mit der (gemeinsamen) Dichte
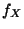 . Dann ist auch die Zufallsvariable
. Dann ist auch die Zufallsvariable 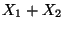 absolutstetig, und ihre Dichte ist gegeben durch
absolutstetig, und ihre Dichte ist gegeben durch
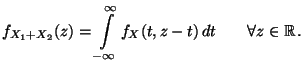 |
(32) |
Falls die Zufallsvariablen 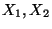 unabhängig sind, dann gilt
insbesondere die sogenannte Faltungsformel
unabhängig sind, dann gilt
insbesondere die sogenannte Faltungsformel
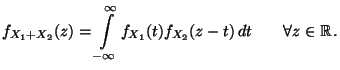 |
(33) |
- Beweis
 Wir benutzen die Tatsache, daß zwischen
Verteilungsfunktion und Dichte einer Zufallsvariablen eine
eineindeutige Zuordnung besteht, und zeigen, daß das Integral
der Funktion in (32)
die Verteilungsfunktion von
Wir benutzen die Tatsache, daß zwischen
Verteilungsfunktion und Dichte einer Zufallsvariablen eine
eineindeutige Zuordnung besteht, und zeigen, daß das Integral
der Funktion in (32)
die Verteilungsfunktion von 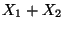 ergibt. Und zwar gilt
für jedes
ergibt. Und zwar gilt
für jedes
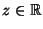
Die Faltungsformel (33) ergibt sich unmittelbar (32), weil
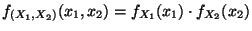 , falls
, falls 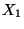 und
und 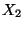 unabhängig sind.
unabhängig sind.
- Beachte
-
Völlig analog zu Theorem 3.22 ergibt sich
- Theorem 3.23
 Die Zufallsvariablen
Die Zufallsvariablen 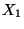 und
und 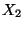 seien
unabhängig und absolutstetig mit den Dichten
seien
unabhängig und absolutstetig mit den Dichten
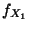 und
und 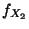 . Dann sind die Zufallsvariablen
. Dann sind die Zufallsvariablen
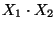 und
und 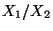 absolutstetig, und ihre
Dichten sind gegeben durch
absolutstetig, und ihre
Dichten sind gegeben durch
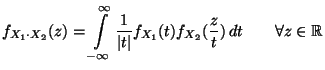 |
(34) |
bzw.
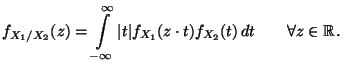 |
(35) |
- Beachte
-
- Der Fall
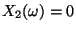 , der bei der Bildung des
Quotienten
, der bei der Bildung des
Quotienten 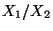 zur Division durch Null führen würde, tritt
nur mit Wahrscheinlichkeit Null auf (weil
zur Division durch Null führen würde, tritt
nur mit Wahrscheinlichkeit Null auf (weil 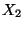 absolutstetig ist).
absolutstetig ist).
- Deshalb kann
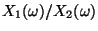 für solche
für solche
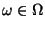 gesondert definiert werden (z.B. können wir dann
gesondert definiert werden (z.B. können wir dann
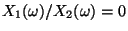 setzen).
setzen).
- Beispiel
 Falls
Falls 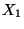 und
und 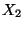 unabhängig sind mit
unabhängig sind mit 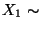 N(0,1) und
N(0,1) und
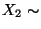 N(0,1), dann gilt
N(0,1), dann gilt
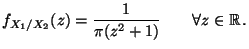 |
(36) |
denn aus (35) ergibt sich, daß
- Beachte
 Eine absolutstetige Zufallsvariable
mit der in (36) gegebenen Dichte heißt Cauchy-verteilt.
Eine absolutstetige Zufallsvariable
mit der in (36) gegebenen Dichte heißt Cauchy-verteilt.




Next: Weitere Charakteristiken von Zufallsvariablen;
Up: Funktionen von Zufallsvariablen
Previous: Quadrierung
Contents
Roland Maier
2001-08-20
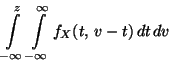
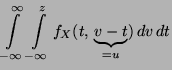
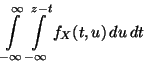
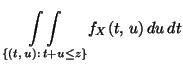
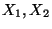 unabhängig sind mit
unabhängig sind mit
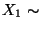 N
N
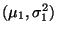 bzw.
bzw. 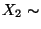 N
N
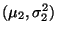 , dann ergibt sich aus (33), daß auch
die Summe
, dann ergibt sich aus (33), daß auch
die Summe 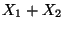 normalverteilt ist mit
normalverteilt ist mit
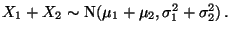

 von
unabhängigen Zufallsvariablen
von
unabhängigen Zufallsvariablen
 mit
mit 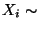 N
N
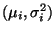 für alle
für alle
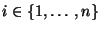 , daß
, daß