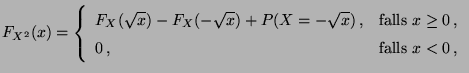Next: Summe, Produkt und Quotient
Up: Funktionen von Zufallsvariablen
Previous: Lineare Transformation
Contents
Quadrierung
- Theorem 3.21
 Sei
Sei
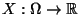 eine beliebige Zufallsgröße.
Dann gilt
eine beliebige Zufallsgröße.
Dann gilt
- für die Verteilungsfunktion von
- falls
 absolutstetig ist mit der Dichte
absolutstetig ist mit der Dichte 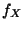 , dann ist auch
, dann ist auch
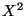 absolutstetig, und es gilt
absolutstetig, und es gilt
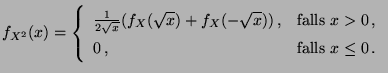 |
(30) |
- Beweis
 analog zum Beweis von Theorem 3.20, wobei
jetzt
analog zum Beweis von Theorem 3.20, wobei
jetzt
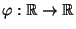 mit
mit
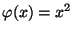 .
.
- Beispiel
 Falls
Falls
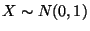 , dann ergibt sich aus
(30):
, dann ergibt sich aus
(30):
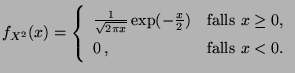 |
(31) |
- Beachte
 Die Summe von unabhängigen (und identisch verteilten)
Zufallsvariablen,
deren Dichte durch (31) gegeben ist,
heißt
Die Summe von unabhängigen (und identisch verteilten)
Zufallsvariablen,
deren Dichte durch (31) gegeben ist,
heißt 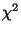 -verteilt. Die
-verteilt. Die 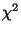 -Verteilung ist
eine sogenannte statistische Prüfverteilung, die
im weiteren Verlauf der Vorlesung noch genauer diskutiert
wird.
-Verteilung ist
eine sogenannte statistische Prüfverteilung, die
im weiteren Verlauf der Vorlesung noch genauer diskutiert
wird.
Roland Maier
2001-08-20
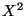
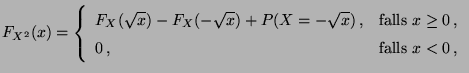
 absolutstetig ist mit der Dichte
absolutstetig ist mit der Dichte 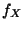 , dann ist auch
, dann ist auch
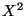 absolutstetig, und es gilt
absolutstetig, und es gilt