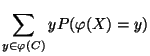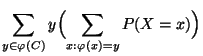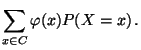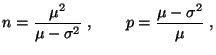Next: Eigenschaften von Erwartungswert und
Up: Momente von Zufallsvariablen
Previous: Erwartungswert
Contents
Varianz und höhere Momente
Es ist klar, daß der Erwartungswert
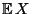 einer (diskreten bzw.
absolutstetigen) Zufallsvariablen
einer (diskreten bzw.
absolutstetigen) Zufallsvariablen  eindeutig durch die
Wahrscheinlichkeitsfunktion bzw. die Dichte von
eindeutig durch die
Wahrscheinlichkeitsfunktion bzw. die Dichte von  bestimmt wird;
vgl. Definition 4.1.
bestimmt wird;
vgl. Definition 4.1.
Umgekehrt ist jedoch im allgemeinen die
Wahrscheinlichkeitsfunktion bzw. die Dichte einer (diskreten bzw.
absolutstetigen) Zufallsvariablen  nicht eindeutig durch
den Erwartungswert
nicht eindeutig durch
den Erwartungswert
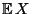 von
von  festgelegt.
festgelegt.
- Beispiel
 (symmetrische diskrete Gleichverteilung)
(symmetrische diskrete Gleichverteilung)
Der Erwartungswert
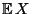 der Zufallsvariablen
der Zufallsvariablen  wird manchmal
auch das erste Moment von
wird manchmal
auch das erste Moment von  genannt. Völlig analog lassen
sich die Begriffe der Varianz bzw. der höheren Momente einer
beliebigen Zufallsvariable
genannt. Völlig analog lassen
sich die Begriffe der Varianz bzw. der höheren Momente einer
beliebigen Zufallsvariable  einführen, und zwar durch die
Betrachtung des Erwartungswertes
einführen, und zwar durch die
Betrachtung des Erwartungswertes
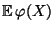 entsprechend
gewählter Funktionen
entsprechend
gewählter Funktionen
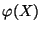 von
von  .
.
In diesem Zusammenhang ist der folgende Hilfssatz nützlich.
- Lemma 4.2
 Sei
Sei
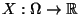 eine beliebige
Zufallsvariable, und sei
eine beliebige
Zufallsvariable, und sei
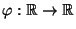 eine stetige
Abbildung.
Dann läßt sich der Erwartungswert
eine stetige
Abbildung.
Dann läßt sich der Erwartungswert
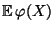 der
Zufallsvariablen
der
Zufallsvariablen
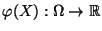 wie folgt
darstellen.
wie folgt
darstellen.
- Falls
 diskret ist mit
diskret ist mit
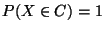 für eine
abzählbare Menge
für eine
abzählbare Menge
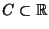 , dann gilt
, dann gilt
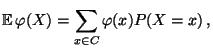 |
(9) |
wobei vorausgesetzt wird, daß
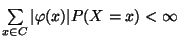 .
.
- Falls
 absolutstetig ist mit der Dichte
absolutstetig ist mit der Dichte 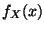 ,
dann gilt
,
dann gilt
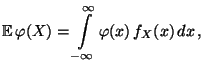 |
(10) |
wobei vorausgesetzt wird, daß
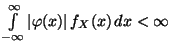 .
.
- Beweis
 Wir zeigen nur die Gültigkeit von
(9). Die Herleitung von (10)
erfordert mathematische Hilfsmittel, die über den Rahmen
dieser einführenden Vorlesung hinausgehen. Sei also
Wir zeigen nur die Gültigkeit von
(9). Die Herleitung von (10)
erfordert mathematische Hilfsmittel, die über den Rahmen
dieser einführenden Vorlesung hinausgehen. Sei also
 diskret ist mit
diskret ist mit
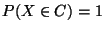 für eine
abzählbare Menge
für eine
abzählbare Menge
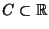 . Dann ist auch
. Dann ist auch
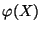 eine diskrete Zufallsvariable mit
wobei
eine diskrete Zufallsvariable mit
wobei
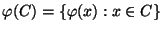 . Aus der
Definition (3) für den Erwartungswert
diskreter Zufallsvariablen ergibt sich somit
. Aus der
Definition (3) für den Erwartungswert
diskreter Zufallsvariablen ergibt sich somit
- Definition 4.3
-
- Beispiele
-
- Binomialverteilung
- Normalverteilung
- Beachte
-
- Beachte
 Sei
Sei
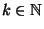 , und sei
, und sei
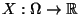 eine beliebige
Zufallsvariable mit
eine beliebige
Zufallsvariable mit
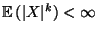 .
.
- Betrachten die Abbildung
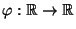 mit
mit
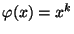 . Dann heißt der Erwartungswert
. Dann heißt der Erwartungswert
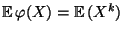 von
von
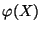 das
das
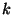 -te Moment von
-te Moment von  .
.
- Betrachten die Abbildung
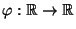 mit
mit
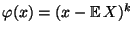 . Dann heißt der Erwartungswert
. Dann heißt der Erwartungswert
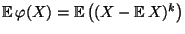 von
von
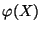 das
das
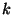 -te zentrale Moment von
-te zentrale Moment von  .
.
- Die Varianz
Var
 ist also das 2. zentrale Moment von
ist also das 2. zentrale Moment von
 .
.
-
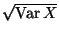 heißt Standardabweichung
von
heißt Standardabweichung
von  .
.




Next: Eigenschaften von Erwartungswert und
Up: Momente von Zufallsvariablen
Previous: Erwartungswert
Contents
Roland Maier
2001-08-20
![]() einer (diskreten bzw.
absolutstetigen) Zufallsvariablen
einer (diskreten bzw.
absolutstetigen) Zufallsvariablen ![]() eindeutig durch die
Wahrscheinlichkeitsfunktion bzw. die Dichte von
eindeutig durch die
Wahrscheinlichkeitsfunktion bzw. die Dichte von ![]() bestimmt wird;
vgl. Definition 4.1.
bestimmt wird;
vgl. Definition 4.1.
![]() nicht eindeutig durch
den Erwartungswert
nicht eindeutig durch
den Erwartungswert
![]() von
von ![]() festgelegt.
festgelegt.
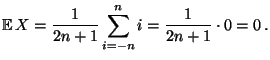
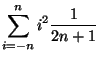
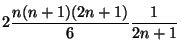
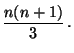
![]() der Zufallsvariablen
der Zufallsvariablen ![]() wird manchmal
auch das erste Moment von
wird manchmal
auch das erste Moment von ![]() genannt. Völlig analog lassen
sich die Begriffe der Varianz bzw. der höheren Momente einer
beliebigen Zufallsvariable
genannt. Völlig analog lassen
sich die Begriffe der Varianz bzw. der höheren Momente einer
beliebigen Zufallsvariable ![]() einführen, und zwar durch die
Betrachtung des Erwartungswertes
einführen, und zwar durch die
Betrachtung des Erwartungswertes
![]() entsprechend
gewählter Funktionen
entsprechend
gewählter Funktionen
![]() von
von ![]() .
.
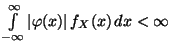 .
.