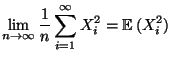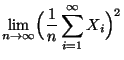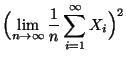Next: Empirische Verteilungsfunktion
Up: Grundideen der statistischen Datenanalyse
Previous: Stichprobenmittel
Contents
Stichprobenvarianz
Wir untersuchen nun die Frage, wie die Varianz
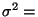 Var
Var  der Stichprobenvariablen
der Stichprobenvariablen  aus den beobachteten Daten
aus den beobachteten Daten
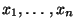 bestimmt werden kann. Dabei gehen wir ähnlich wie
in Abschnitt 5.1.2 vor.
bestimmt werden kann. Dabei gehen wir ähnlich wie
in Abschnitt 5.1.2 vor.
- Definition 5.6
 Die Zufallsvariable
Die Zufallsvariable
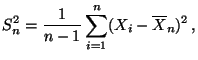 |
(9) |
heißt Stichprobenvarianz der Zufallsstichprobe
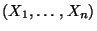 .
.
- Theorem 5.7
 Es gilt
Es gilt
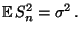 |
(10) |
Falls
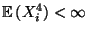 für
für
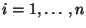 , dann gilt
außerdem
, dann gilt
außerdem
Var 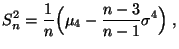 |
(11) |
wobei
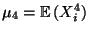 und
und
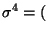 Var
Var 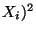 das 4-te
Moment bzw. die quadrierte Varianz der Stichprobenvariablen
das 4-te
Moment bzw. die quadrierte Varianz der Stichprobenvariablen  bezeichnen.
bezeichnen.
- Beweis
-
- Wir zeigen nur die Gültigkeit von (10).
Die Gültigkeit von (11) ergibt sich durch
ähnliche Überlegungen.
- Aus der Definitionsgleichung (9) von
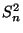 ergibt sich, daß
ergibt sich, daß
- Wegen der Linearität des Erwartungswertes (vgl. Formel
(4.15)) folgt hieraus, daß
wobei sich das vorletzte Gleichheitszeichen aus
(3) und (4) ergibt.
- Damit ist (10) bewiesen.
- Beachte
-
- Weil die Stichprobenvarianz
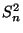 den Erwartungswert
den Erwartungswert 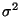 hat (vgl. (10)), kann
hat (vgl. (10)), kann
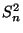 als ein geeigneter Schätzer der (im allgemeinen
unbekannten) Modellcharakteristik
als ein geeigneter Schätzer der (im allgemeinen
unbekannten) Modellcharakteristik 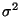 angesehen werden.
angesehen werden.
- Wegen (10) wird bei der Schätzung von
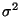 durch
durch
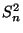 kein systematischer Fehler begangen.
kein systematischer Fehler begangen.
Neben den Formeln (10) und (11) für
Erwartungswert und Varianz des Stichprobenvarianz 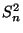 sind
erneut weitere Aussagen über die Verteilung von
sind
erneut weitere Aussagen über die Verteilung von 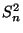 bzw. über
deren asymptotisches Verhalten für große
bzw. über
deren asymptotisches Verhalten für große  von Interesse.
von Interesse.
Aus dem starken Gesetz der großen Zahlen (vgl. Theorem 4.22) bzw.
aus dem zentralen Grenzwertsatz (vgl. Theorem 4.24) ergibt sich
- Theorem 5.8
 Es gilt
Es gilt
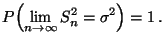 |
(12) |
Falls
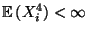 für
für
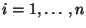 , dann gilt
außerdem
, dann gilt
außerdem
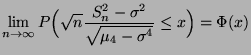 |
(13) |
für jedes
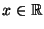 , wobei
, wobei 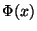 die Verteilungsfunktion der
Standardnormalverteilung ist.
die Verteilungsfunktion der
Standardnormalverteilung ist.
- Beweis
-
- Wir zeigen nur die Gültigkeit von (12).
Die Herleitung von (13) erfordert
Hilfsmittel, die über den Rahmen dieser einführenden
Vorlesung hinausgehen.
- Im Beweis von Theorem 5.7 hatten wir gezeigt, daß
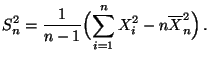 |
(14) |
- Außerdem kann man zeigen, daß die Unabhängigkeit und identische
Verteiltheit der
Stichprobenvariablen
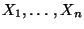 impliziert, daß auch die
Zufallsvariablen
impliziert, daß auch die
Zufallsvariablen
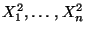 unabhängig und identisch
veteilt sind.
unabhängig und identisch
veteilt sind.
- Deshalb ergibt sich aus dem starken Gesetz der großen Zahlen
(vgl. Theorem 4.22), daß mit Wahrscheinlichkeit 1
und
- Hieraus und aus (14) ergibt sich (12).




Next: Empirische Verteilungsfunktion
Up: Grundideen der statistischen Datenanalyse
Previous: Stichprobenmittel
Contents
Roland Maier
2001-08-20
![]() Var
Var ![]() der Stichprobenvariablen
der Stichprobenvariablen ![]() aus den beobachteten Daten
aus den beobachteten Daten
![]() bestimmt werden kann. Dabei gehen wir ähnlich wie
in Abschnitt 5.1.2 vor.
bestimmt werden kann. Dabei gehen wir ähnlich wie
in Abschnitt 5.1.2 vor.
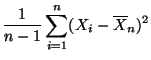
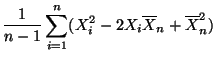
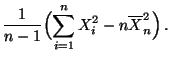
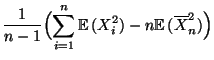
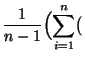 Var
Var 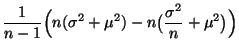
![]() sind
erneut weitere Aussagen über die Verteilung von
sind
erneut weitere Aussagen über die Verteilung von ![]() bzw. über
deren asymptotisches Verhalten für große
bzw. über
deren asymptotisches Verhalten für große ![]() von Interesse.
von Interesse.