



Next: Stichprobenvarianz
Up: Grundideen der statistischen Datenanalyse
Previous: Zufallsstichprobe
Contents
Stichprobenmittel
Wir diskutieren zunächst die Frage, wie der Erwartungswert
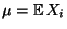 der Stichprobenvariablen
der Stichprobenvariablen  aus den beobachteten
Daten
aus den beobachteten
Daten
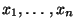 bestimmt werden kann.
bestimmt werden kann.
- Definiton 5.3
 Die Zufallsvariable
Die Zufallsvariable
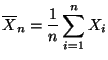 |
(2) |
heißt Stichprobenmittel der Zufallsstichprobe
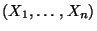 .
.
In Abschnitt 4.3.2 hatten wir uns überlegt (vgl. den
Beweis von Theorem 4.20), daß sich Erwartungswert und Varianz von
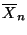 wie folgt darstellen lassen.
wie folgt darstellen lassen.
- Theorem 5.4
 Es gilt
Es gilt
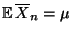 |
(3) |
und
Var 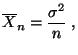 |
(4) |
wobei
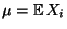 und
und
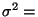 Var
Var  den Erwartungswert
bzw. die Varianz der Stichprobenvariablen
den Erwartungswert
bzw. die Varianz der Stichprobenvariablen  bezeichnen.
bezeichnen.
- Beachte
-
- Weil das Stichprobenmittel
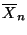 den Erwartungswert
den Erwartungswert 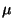 hat (vgl. (3)),
kann man
hat (vgl. (3)),
kann man
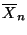 als einen geeigneten
,,Schätzer'' der (im allgemeinen unbekannten) Modellcharakteristik
als einen geeigneten
,,Schätzer'' der (im allgemeinen unbekannten) Modellcharakteristik
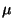 ansehen.
ansehen.
- Wegen (3) sagt man, daß bei der Schätzung von
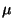 durch
durch
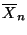 kein ,,systematischer Fehler'' begangen wird.
kein ,,systematischer Fehler'' begangen wird.
- Der Schätzer
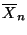 kann dennoch
sehr ungenau sein, wobei man den in (4)
gegebenen Wert
kann dennoch
sehr ungenau sein, wobei man den in (4)
gegebenen Wert
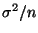 als Kennzahl für die
Schätzgenauigkeit von
als Kennzahl für die
Schätzgenauigkeit von
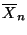 auffassen kann.
auffassen kann.
- Insbesondere bedeutet (4), daß die
Schätzgenauigkeit mit wachsendem Stichprobenumfang
 verbessert wird.
verbessert wird.
- Dabei ist jedoch zu beachten, daß
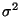 im allgemeinen
ebenfalls unbekannt ist.
im allgemeinen
ebenfalls unbekannt ist.
- Um die Schätzgenauigkeit von
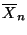 bei vorgegebenem
Stichprobenumfang
bei vorgegebenem
Stichprobenumfang  bestimmen zu können, muß deshalb auch
bestimmen zu können, muß deshalb auch
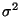 aus den beobachteten Daten
aus den beobachteten Daten
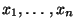 geschätzt werden.
geschätzt werden.
- Diese Fragestellung werden wir in Abschnitt 5.1.3 diskutieren.
Neben den Formeln (3) und (4) für
Erwartungswert und Varianz des Stichprobenmittels
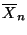 sind noch weitere Aussagen über die Verteilung von
sind noch weitere Aussagen über die Verteilung von
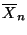 von Interesse bzw. über deren asymptotisches Verhalten für große
von Interesse bzw. über deren asymptotisches Verhalten für große
 .
.
Aus dem starken Gesetz der großen Zahlen (vgl. Theorem 4.22) bzw.
aus dem zentralen Grenzwertsatz (vgl. Theorem 4.24) ergibt sich
unmittelbar
- Theorem 5.5
 Es gilt
Es gilt
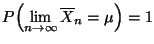 |
(5) |
und
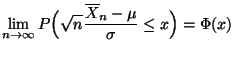 |
(6) |
für jedes
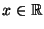 , wobei
, wobei 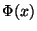 die Verteilungsfunktion der
Standardnormalverteilung ist.
die Verteilungsfunktion der
Standardnormalverteilung ist.
- Beispiel
-




Next: Stichprobenvarianz
Up: Grundideen der statistischen Datenanalyse
Previous: Zufallsstichprobe
Contents
Roland Maier
2001-08-20
![]() der Stichprobenvariablen
der Stichprobenvariablen ![]() aus den beobachteten
Daten
aus den beobachteten
Daten
![]() bestimmt werden kann.
bestimmt werden kann.
![]() wie folgt darstellen lassen.
wie folgt darstellen lassen.
![]() sind noch weitere Aussagen über die Verteilung von
sind noch weitere Aussagen über die Verteilung von
![]() von Interesse bzw. über deren asymptotisches Verhalten für große
von Interesse bzw. über deren asymptotisches Verhalten für große
![]() .
.