- Sei
![$ F:\mathbb{R}\to[0,1]$](img394.png) eine beliebige Verteilungsfunktion.
eine beliebige Verteilungsfunktion.
- Die Funktion
![$ F^{-1}:[0,1]\to\mathbb{R}$](img1588.png) mit
mit
heißt Quantilfunktion der Verteilungsfunktion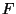 (bzw. der
zugehörigen Verteilung).
(bzw. der
zugehörigen Verteilung).
- Sei
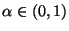 . Die Zahl
. Die Zahl
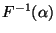 wird dann
wird dann
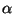 -Quantil von
-Quantil von 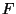 genannt.
genannt.
- Wenn
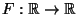 eine beliebige monoton wachsende rechtsstetige
Funktion ist (die nicht unbedingt eine Verteilungsfunktion sein
muß), dann heißt die in (5) definierte Funktion
eine beliebige monoton wachsende rechtsstetige
Funktion ist (die nicht unbedingt eine Verteilungsfunktion sein
muß), dann heißt die in (5) definierte Funktion
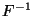 verallgemeinerte inverse Funktion von
verallgemeinerte inverse Funktion von 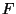 .
.
- Quantilfunktionen sind also spezielle verallgemeinerte inverse Funktionen.
Um Konfidenzintervalle für die Parameter von normalverteilten Stichprobenvariablen konstruieren zu können, werden insbesondere die Quantilfunktionen der Standardnormalverteilung, der
- Quantile der N
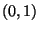 -Verteilung
-Verteilung
- Das
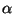 -Quantil der Verteilungsfunktion
-Quantil der Verteilungsfunktion 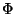 (d.h. der
Standardnormalverteilung N
(d.h. der
Standardnormalverteilung N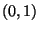 ) wird mit
) wird mit 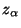 bezeichnet.
bezeichnet.
- Mit anderen Worten: Für jedes
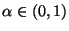 ist
ist 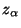 die
Lösung der Quantilgleichung
die
Lösung der Quantilgleichung
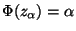 .
.
- Für
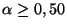 kann man das
kann man das 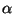 -Quantil
-Quantil 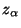 aus
Tabelle 1 entnehmen; vgl. Abschnitt 5.
aus
Tabelle 1 entnehmen; vgl. Abschnitt 5.
- Aus der Symmetrieeigenschaft
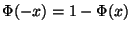 für jedes
für jedes
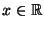 ergibt sich außerdem, daß für jedes
ergibt sich außerdem, daß für jedes
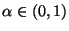
- Das
- Quantile der
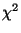 -Verteilung mit
-Verteilung mit 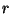 Freiheitsgraden
Freiheitsgraden
- Die Zufallsvariable
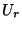 sei
sei 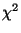 -verteilt mit
-verteilt mit
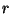 -Freiheitsgraden, d.h.,
-Freiheitsgraden, d.h.,
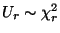 .
.
- Für
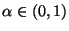 sei
sei
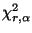 die (eindeutig
bestimmte) Lösung der Gleichung
die (eindeutig
bestimmte) Lösung der Gleichung
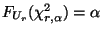 , wobei die Dichte
, wobei die Dichte 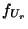 von
von 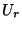 in Theorem 1.6 gegeben ist.
in Theorem 1.6 gegeben ist.
- Dann heißt
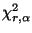 das
das 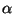 -Quantil der
-Quantil der
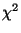 -Verteilung mit
-Verteilung mit 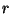 Freiheitsgraden.
Freiheitsgraden.
- Quantile der
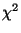 -Verteilung mit
-Verteilung mit 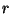 Freiheitsgraden sind in
Tabelle 2 gegeben, vgl. Abschnitt 5.
Freiheitsgraden sind in
Tabelle 2 gegeben, vgl. Abschnitt 5.
- Die Zufallsvariable
- Quantile der t-Verteilung mit
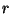 Freiheitsgraden
Freiheitsgraden
- Die Zufallsvariable
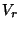 sei t-verteilt mit
sei t-verteilt mit 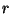 -Freiheitsgraden,
d.h.,
-Freiheitsgraden,
d.h., 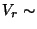 t
t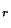 , wobei die Dichte
, wobei die Dichte 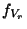 von
von 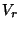 in Theorem 1.12 gegeben ist.
in Theorem 1.12 gegeben ist.
- Für
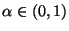 wird dann die Lösung
wird dann die Lösung
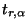 der
Gleichung
der
Gleichung
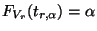 das
das 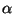 -
Quantil der t-Verteilung mit
-
Quantil der t-Verteilung mit 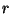 Freiheitsgraden genannt, vgl.
Tabelle 3 in Abschnitt 5.
Freiheitsgraden genannt, vgl.
Tabelle 3 in Abschnitt 5.
- Analog zu der Symmetrieeigenschaft
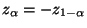 der
Quantile
der
Quantile 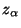 der N
der N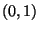 -Verteilung gilt auch
-Verteilung gilt auch
für beliebige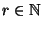 und
und
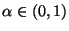 .
.
- Die Zufallsvariable