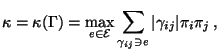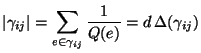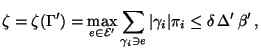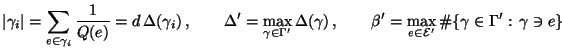Nächste Seite: Monte-Carlo-Simulation
Aufwärts: Abschätzung der Konvergenzgeschwindigkeit; Reversibilität
Vorherige Seite: Dirichlet-Formen und Rayleigh-Theorem
Inhalt
Schranken für die Eigenwerte 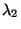 und
und
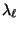
Um Schranken für die Eigenwerte 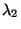 und
und
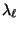 herzuleiten, benötigen wir nun noch die folgenden Begriffe und
Bezeichnungen.
herzuleiten, benötigen wir nun noch die folgenden Begriffe und
Bezeichnungen.
Theorem 2.18

Für die Eigenwerte
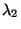
und
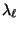
von

gilt
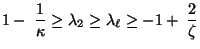 |
(123) |
und somit
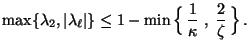 |
(124) |
- Beweis
-
- Wir zeigen zunächst, dass
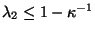 .
.
- Wegen Theorem 2.17 genügt es zu zeigen, dass
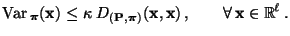 |
(125) |
- Mit den in (119) eingeführten Bezeichnungen gilt
- Aus der Ungleichung von Cauchy-Schwarz ergibt sich nun, dass
wobei sich die letzte Ungleichung aus Lemma 2.8 und
aus der Definitionsgleichung (120) des
Poincaré-Koeffizienten ergibt. Damit ist (125)
bewiesen.
- Um den Beweis zu beenden, ist noch zu zeigen, dass
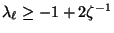 .
.
- Hierfür nutzen wir die folgende Identität: Für jedes
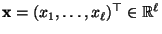 gilt
gilt
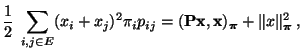 |
(126) |
denn aus der Reversibilität von
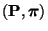 ergibt sich, dass
ergibt sich, dass
- Sei nun
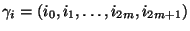 mit
mit
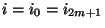 ein Pfad von
ein Pfad von 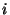 nach
nach 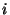 , der eine ungerade
Anzahl von Kanten enthält, so dass keine der Kanten mehrfach
auftritt.
, der eine ungerade
Anzahl von Kanten enthält, so dass keine der Kanten mehrfach
auftritt.
- Dann gilt
wobei 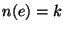 , falls
, falls
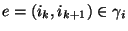 .
.
- Deshalb ergibt sich (ähnlich wie im ersten Teil des Beweises) aus
der Ungleichung von Cauchy-Schwarz, dass für jedes
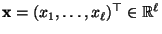
- Hieraus und aus (126) ergibt sich nun, dass
- Für
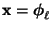 gilt also insbesondere
gilt also insbesondere
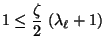
bzw.
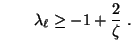

- Beispiel
 Zufällige Irrfahrten auf Graphen
Zufällige Irrfahrten auf Graphen
- Wir kehren nun zu dem bereits in Abschnitt 2.3.1
diskutierten Beispiel von zufälligen Irrfahrten auf Graphen
zurück.
- Sei also
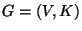 ein verbundener Graph mit der Menge
ein verbundener Graph mit der Menge
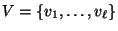 von
von 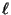 Eckpunkten und der Menge
Eckpunkten und der Menge 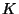 von Kanten, die jeweils zwei Eckpunkte miteinander verbinden,
von Kanten, die jeweils zwei Eckpunkte miteinander verbinden,
- so dass es für jedes Paar
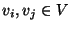 von Eckpunkten einen
,,Pfad'' von Kanten aus
von Eckpunkten einen
,,Pfad'' von Kanten aus 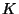 gibt, der die Kanten
gibt, der die Kanten 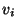 und
und 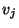 miteinander verbindet.
miteinander verbindet.
- Eine zufällige Irrfahrt auf dem Graph
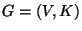 ist eine
Markov-Kette
ist eine
Markov-Kette
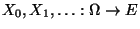
- Wir hatten gezeigt, dass
- Für den in (120) eingeführten Poincaré-Koeffizienten
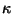 gilt dann
wobei
und
gilt dann
wobei
und
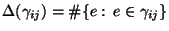 die Anzahl
der Kanten (d.h. die Länge) des Pfades
die Anzahl
der Kanten (d.h. die Länge) des Pfades
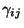 bezeichnet.
bezeichnet.
- Hieraus und aus (127)-(128)
ergibt sich, dass
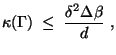 |
(129) |
wobei 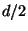 die Gesamtanzahl aller Kanten,
die Gesamtanzahl aller Kanten,
-
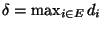 die maximale Anzahl von Kanten ist, die
von einem Eckpunkt ausgehen,
die maximale Anzahl von Kanten ist, die
von einem Eckpunkt ausgehen,
-
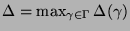 die maximale
Pfadlänge und
die maximale
Pfadlänge und
-
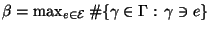 der
sogenannte Bottleneck-Koeffizient, d.h., die maximale Anzahl
der Pfade ist, die jeweils durch eine einzelne Kante laufen.
der
sogenannte Bottleneck-Koeffizient, d.h., die maximale Anzahl
der Pfade ist, die jeweils durch eine einzelne Kante laufen.
- Aus (123) und (129) ergibt sich nun
die folgende Abschätzung
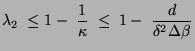 |
(130) |
für den zweitgrößten Eigenwert 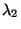 von
von
 .
.
- Auf ähnliche Weise ergibt sich die Abschätzung
wobei
und somit
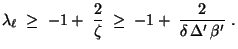 |
(131) |
- Beachte
- Für das bereits in Abschnitt 2.3.1
betrachtete Zahlenbeispiel
gilt insbesondere, dass
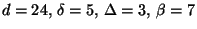
und
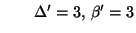
- Aus (130) und (131) ergibt sich somit
bzw.




Nächste Seite: Monte-Carlo-Simulation
Aufwärts: Abschätzung der Konvergenzgeschwindigkeit; Reversibilität
Vorherige Seite: Dirichlet-Formen und Rayleigh-Theorem
Inhalt
Ursa Pantle
2003-09-29
![]() und
und
![]() herzuleiten, benötigen wir nun noch die folgenden Begriffe und
Bezeichnungen.
herzuleiten, benötigen wir nun noch die folgenden Begriffe und
Bezeichnungen.
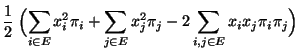
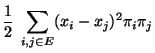
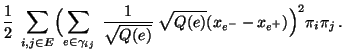
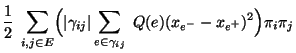
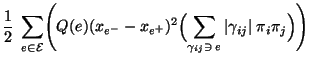
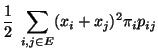
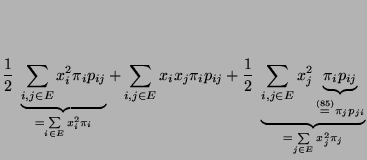
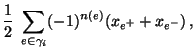
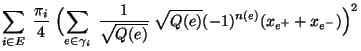
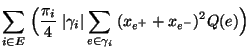
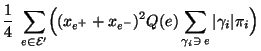
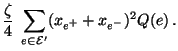
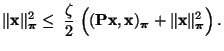
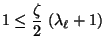 bzw.
bzw.