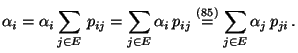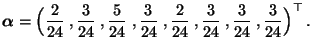Nächste Seite: Rekursive Konstruktion der ,,Vergangenheit''
Aufwärts: Abschätzung der Konvergenzgeschwindigkeit; Reversibilität
Vorherige Seite: Abschätzung der Konvergenzgeschwindigkeit; Reversibilität
Inhalt
Definition und Beispiele
Wir leiten zunächst eine einfache Charakterisierung der
Reversibilität von stationären (jedoch nicht unbedingt
ergodischen) Markov-Ketten her.
- Beweis
-
- Die Notwendigkeit der Bedingung (85) ergibt sich
unmittelbar aus der Definitionsgleichung (84). Aus
(84) folgt nämlich insbesondere, dass
- Somit gilt auch
- Wenn umgekehrt (85) gilt, dann ergibt sich aus der
Definitionsgleichung (3) von Markov-Ketten, dass
- Damit ist die Gültigkeit von (84) bewiesen.

- Beachte
-
- Im Beweis von Theorem 2.13 wird nicht benötigt,
- dass die stationäre Markov-Kette
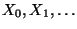 ergodisch ist,
ergodisch ist,
- sondern lediglich, dass sämtliche Komponenten
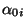 der
stationären Anfangangsveteilung
der
stationären Anfangangsveteilung
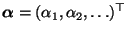 positiv sind.
positiv sind.
- Mit anderen Worten
- Falls die Übergangsmatrix
 nicht irreduzibel oder nicht
aperiodisch ist und somit die Grenzverteilung
nicht irreduzibel oder nicht
aperiodisch ist und somit die Grenzverteilung
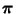 nicht
existiert bzw. nicht eindeutig bestimmt ist,
nicht
existiert bzw. nicht eindeutig bestimmt ist,
- dann bleibt die Gültigkeit von Theorem 2.13 dennoch
erhalten, wenn
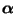 eine beliebige stationäre
Anfangsverteilung ist mit
eine beliebige stationäre
Anfangsverteilung ist mit
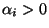 für jedes
für jedes 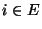 .
.
- Weil
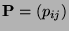 eine stochastische Matrix ist, ergibt sich
aus (85), dass für beliebige
eine stochastische Matrix ist, ergibt sich
aus (85), dass für beliebige 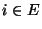
- Mit anderen Worten: Jede Anfangsverteilung
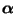 , die
der sogenannten Detailed-Balance-Bedingung
(85) genügt, ist notwendigerweise eine stationäre
Anfangsverteilung, d.h., sie genügt dann auch der ,,globalen''
Balance-Bedingung
, die
der sogenannten Detailed-Balance-Bedingung
(85) genügt, ist notwendigerweise eine stationäre
Anfangsverteilung, d.h., sie genügt dann auch der ,,globalen''
Balance-Bedingung
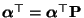 .
.
- Beispiele
-
- Diffusionsmodell
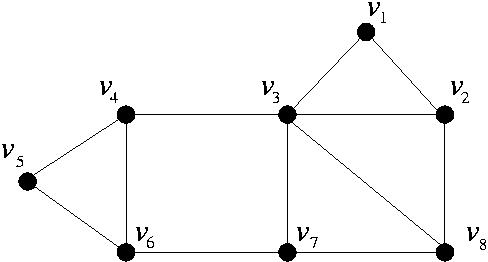
- Wir kehren zu dem bereits in Abschnitt 2.2.3
betrachteten Diffusionsmodell mit dem endlichen Zustandsraum
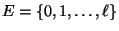 , der irreduziblen (jedoch nicht
aperiodischen) Übergangsmatrix
, der irreduziblen (jedoch nicht
aperiodischen) Übergangsmatrix
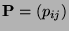 , wobei
, wobei
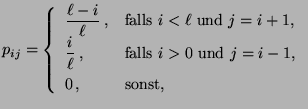 |
(86) |
und der (gemäß Theorem 2.10 eindeutig bestimmten,
jedoch nicht ergodischen) stationären Anfangsverteilung
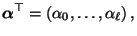 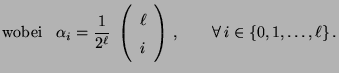 |
(87) |
- Man kann zeigen, dass dann
für beliebige
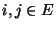 gilt, d.h., das in (86)
bzw. (87) gegebene Paar
gilt, d.h., das in (86)
bzw. (87) gegebene Paar
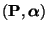 ist
reversibel.
ist
reversibel.
- Geburts- und Todesprozesse
- Zufällige Irrfahrten auf Graphen
- Zyklische zufällige Irrfahrten
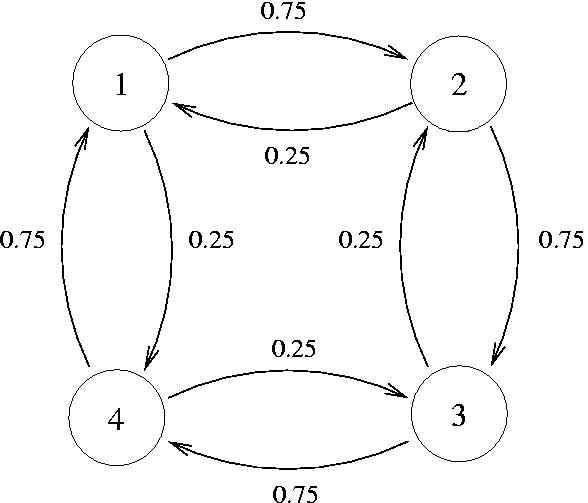
- Das folgende Beispiel einer zyklischen zufälligen Irrfahrt ist
nicht reversibel.
- Dabei sei
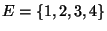 und
und
![$\displaystyle {\mathbf{P}}=\left(\begin{array}{cccc} 0 & 0.75 & 0 & 0.25 \\ [3...
...\ [3\jot] 0 & 0.25 & 0& 0.75\\ [3\jot] 0.75 & 0 & 0.25 & 0 \end{array}\right)$](img735.png) |
(90) |
- d.h., der Übergangsgraph ist gegeben durch
- Die in (90) gegebene Übergangsmatrix ist offenbar
irreduzibel, jedoch nicht aperiodisch, und die (wegen
Theorem 2.10 eindeutig bestimmte) Anfangsverteilung
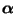 ist gegeben durch
ist gegeben durch
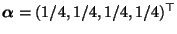 .
.
- Andererseits gilt jedoch
- Es ist intuitiv klar, warum diese zyklische zufällige Irrfahrt
nicht reversibel ist, denn die ,,Fortbewegung'' im Uhrzeigersinn
ist viel wahrscheinlicher als die ,,Fortbewegung'' gegen den
Uhrzeigersinn.
- Doppelt-stochastische Übergangsmatrix




Nächste Seite: Rekursive Konstruktion der ,,Vergangenheit''
Aufwärts: Abschätzung der Konvergenzgeschwindigkeit; Reversibilität
Vorherige Seite: Abschätzung der Konvergenzgeschwindigkeit; Reversibilität
Inhalt
Ursa Pantle
2003-09-29