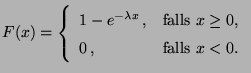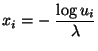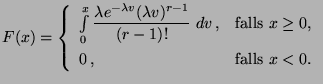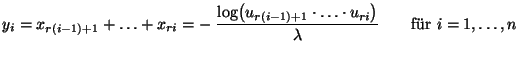Nächste Seite: Transformationsalgorithmen für diskrete Verteilungen
Aufwärts: Transformation gleichverteilter Pseudozufallszahlen
Vorherige Seite: Transformation gleichverteilter Pseudozufallszahlen
Inhalt
Inversionsmethode
- Als eine Grundlage zur Erzeugung von Pseudozufallszahlen
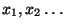 , die als Realisierungen von Zufallsvariablen
, die als Realisierungen von Zufallsvariablen
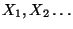 aufgefasst werden können,
aufgefasst werden können,
- deren Verteilungsfunktion
![$ F:\mathbb{R}\to[0,1]$](img1223.png) eine beliebige monoton
nichtfallende und rechtsseitig stetige Funktion ist mit
eine beliebige monoton
nichtfallende und rechtsseitig stetige Funktion ist mit
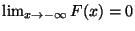 und
und
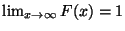 ,
,
- kann die folgende Eigenschaft der verallgemeinerten Inversen
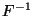 von
von 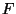 verwendet werden.
verwendet werden.
- Zur Erinnerung
Theorem 3.4
- Sei
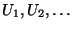 eine Folge von unabhängigen und
eine Folge von unabhängigen und
![$ (0,1]$](img167.png) -gleichverteilten Zufallsvariablen, und sei
-gleichverteilten Zufallsvariablen, und sei
![$ F:\mathbb{R}\to[0,1]$](img1223.png) eine beliebige Verteilungsfunktion.
eine beliebige Verteilungsfunktion.
- Dann sind die Zufallsvariablen
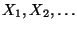 mit
mit
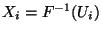 für jedes
für jedes
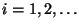 unabhängig und besitzen
die Verteilungsfunktion
unabhängig und besitzen
die Verteilungsfunktion 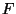 .
.
- Beweis
-
- Beispiele
-
- Wir diskutieren nun einige Beispiele, die verdeutlichen,
- wie Theorem 3.4 genutzt werden kann, um
Pseudozufallszahlen
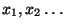 zu erzeugen,
zu erzeugen,
- die als Realisierungen von unabhängigen Zufallsvariablen
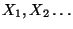 mit einer vorgegebenen Verteilungsfunktion
mit einer vorgegebenen Verteilungsfunktion
![$ F:\mathbb{R}\to[0,1]$](img1223.png) aufgefasst werden können.
aufgefasst werden können.
- Wir sprechen dann kurz von
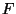 -verteilten Pseudozufallszahlen
-verteilten Pseudozufallszahlen
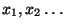 ,
,
- obwohl die empirische Veteilungsfunktion
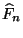 der
(konkreten) Stichprobe
der
(konkreten) Stichprobe
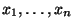
- selbst für große
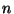 natürlich nur näherungsweise mit
natürlich nur näherungsweise mit 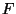 übereinstimmt.
übereinstimmt.
- Dabei kann Theorem 3.4 nur dann direkt
angewendet werden, wenn
- sich die verallgemeinerte inverse Funktion
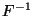 von
von 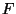 explizit (d.h. durch eine geschlossene Formel) bestimmen lässt,
explizit (d.h. durch eine geschlossene Formel) bestimmen lässt,
- was jedoch eher eine Ausnahmesituation ist.
- Exponentialverteilung
- Erlang-Verteilung
- Normalverteilung




Nächste Seite: Transformationsalgorithmen für diskrete Verteilungen
Aufwärts: Transformation gleichverteilter Pseudozufallszahlen
Vorherige Seite: Transformation gleichverteilter Pseudozufallszahlen
Inhalt
Ursa Pantle
2003-09-29
![$ F:\mathbb{R}\to[0,1]$](img1223.png) eine beliebige monoton
nichtfallende und rechtsseitig stetige Funktion ist mit
eine beliebige monoton
nichtfallende und rechtsseitig stetige Funktion ist mit
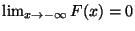 und
und
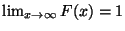 ,
,
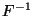 von
von 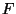 verwendet werden.
verwendet werden.
![$ F:\mathbb{R}\to[0,1]$](img1223.png) eine beliebige Verteilungsfunktion. Dann heißt
die Funktion
eine beliebige Verteilungsfunktion. Dann heißt
die Funktion
![$ F^{-1}:(0,1]\to\mathbb{R}\cup\{\infty\}$](img1228.png) mit
mit
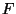 (bzw. der zugehörigen Verteilung).
(bzw. der zugehörigen Verteilung).
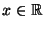 und
und 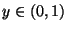 gilt
gilt