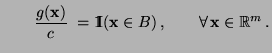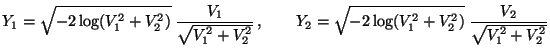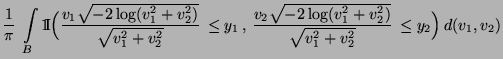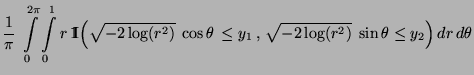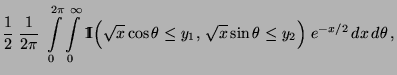Nächste Seite: Quotienten von gleichverteilten Zufallsvariablen
Aufwärts: Transformation gleichverteilter Pseudozufallszahlen
Vorherige Seite: Transformationsalgorithmen für diskrete Verteilungen
Inhalt
Akzeptanz- und Verwerfungsmethode
- Wir diskutieren nun eine weitere Methode, mit der man
Pseudozufallszahlen
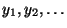 erzeugen kann,
erzeugen kann,
- Wir betrachten zunächst den diskreten Fall.
Theorem 3.5
- Sei
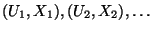 eine Folge von unabhängigen und
identisch verteilten Zufallsvektoren, deren Komponenten unabhängig
sind, wobei
eine Folge von unabhängigen und
identisch verteilten Zufallsvektoren, deren Komponenten unabhängig
sind, wobei 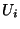 eine
eine ![$ (0,1]$](img167.png) -gleichverteilte Zufallsvariable und
-gleichverteilte Zufallsvariable und
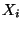 gemäß
gemäß
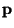 verteilt ist.
verteilt ist.
- Dann ist
- Beweis
-
- Beachte
-
- Aus Theorem 3.5 ergibt sich, dass im Mittel
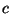 Pseudozufallszahlen erforderlich sind, die
Pseudozufallszahlen erforderlich sind, die 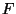 -verteilt sind, um
eine
-verteilt sind, um
eine 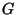 -verteilte Pseudozufallszahl zu erzeugen.
-verteilte Pseudozufallszahl zu erzeugen.
- Wenn mehrere Alternativen für die Wahl der Verteilungsfunktion
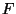 zur Verfügung stehen,
zur Verfügung stehen,
- die ähnlich günstige Eigenschaften hinsichtlich der Erzeugung von
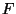 -verteilten Pseudozufallszahlen aufweisen,
-verteilten Pseudozufallszahlen aufweisen,
- dann sollte somit diejenige Verteilungsfunktion
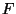 gewählt
werden, für die
gewählt
werden, für die 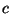 am kleinsten ist.
am kleinsten ist.
- Außerdem ergibt sich aus Theorem 3.5,
- dass die Werte
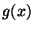 bzw.
bzw. 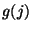 der Dichte in
(19) bzw. (20) nicht
vollständig,
der Dichte in
(19) bzw. (20) nicht
vollständig,
- sondern nur bis auf einen konstanten Proportionalitätsfaktor
bekannt sein müssen.
Im allgemeinen (d.h. nicht notwendig diskreten) Fall kann man
ähnlich vorgehen, wobei das folgende Resultat als Grundlage zur
Konstruktion von Akzeptanz- und Verwerfungsalgorithmen dient.
- Beweis
-
Auf die gleiche Weise ergibt sich die folgende vektorielle Version
von Theorem 3.6.
- Beispiele
-
- Gleichverteilung in beschränkten Borel-Mengen
- Normalverteilung




Nächste Seite: Quotienten von gleichverteilten Zufallsvariablen
Aufwärts: Transformation gleichverteilter Pseudozufallszahlen
Vorherige Seite: Transformationsalgorithmen für diskrete Verteilungen
Inhalt
Ursa Pantle
2003-09-29
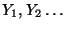 mit einer vorgegebenen
Verteilungsfunktion
mit einer vorgegebenen
Verteilungsfunktion 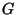 aufgefasst werden können,
aufgefasst werden können,
![$ (0,1]$](img167.png) -gleichverteilten)
Pseudozufallszahlen
-gleichverteilten)
Pseudozufallszahlen
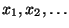 ausgegangen wird,
ausgegangen wird,
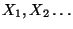 mit einer gewissen
Verteilungsfunktion
mit einer gewissen
Verteilungsfunktion 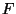 sind,
sind,
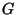 absolutstetig bezüglich
absolutstetig bezüglich 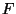 ist, wobei die
Dichte
ist, wobei die
Dichte
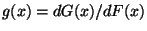 beschränkt ist,
beschränkt ist,
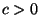 mit
mit
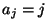 für jedes
für jedes
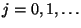 , und seien
, und seien
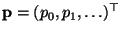 bzw.
bzw.
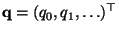 zwei beliebige Wahrscheinlichkeitsfunktionen, so dass für jedes
zwei beliebige Wahrscheinlichkeitsfunktionen, so dass für jedes
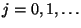 aus
aus 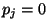 die Gültigkeit von
die Gültigkeit von 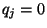 folgt.
folgt.
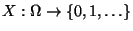 eine Zufallsvariable mit
eine Zufallsvariable mit
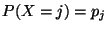 für jedes
für jedes
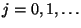 ,
,
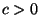 eine positive Zahl, so dass
eine positive Zahl, so dass
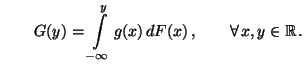
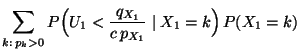
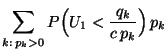
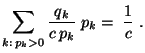
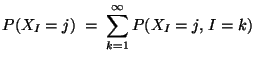
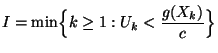
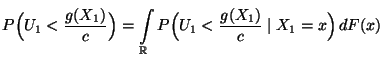
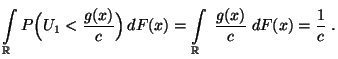
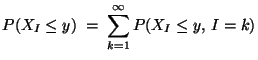
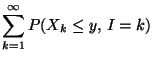
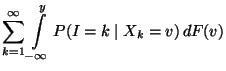
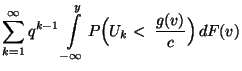
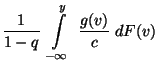
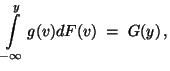
![$\displaystyle \qquad G({\mathbf{y}})=\int\limits_{(-\infty,{\mathbf{y}}]} g({\m...
...dF({\mathbf{x}})\,,\qquad \forall\, {\mathbf{x}},{\mathbf{y}}\in\mathbb{R}^m\,.$](img1415.png)
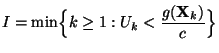
![$\displaystyle G({\mathbf{y}})=\int\limits_{(-\infty,{\mathbf{y}}]}\;\frac{{1\hs...
...}{\vert B\vert}\;dF({\mathbf{x}})\,,\qquad\forall\,{\mathbf{y}}\in\mathbb{R}^m
$](img1424.png)
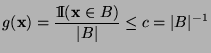 bzw.
bzw.