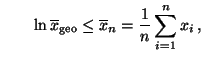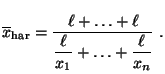Next: Maßzahlen für die Streuung
Up: Kenngrößen zur Beschreibung von
Previous: Kenngrößen zur Beschreibung von
Contents
Lagemaßzahlen
In diesem Abschnitt betrachten wir eine spezielle Klasse von
Kenngrößen der Stichprobe
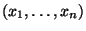 , sogenannte Maßzahlen, die die Lage der Daten beschreiben und die kurz Lagemaßzahlen genannt werden.
, sogenannte Maßzahlen, die die Lage der Daten beschreiben und die kurz Lagemaßzahlen genannt werden.
- Stichprobenmittel
- Wir betrachten zunächst die Stichprobenfunktion
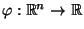 mit
mit
 |
(2) |
d.h., wir betrachten das arithmetische Mittel
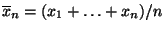 der Stichprobenwerte
der Stichprobenwerte
 .
.
- Die Zahl
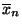 wird Stichprobenmittel der
(konkreten) Stichprobe
wird Stichprobenmittel der
(konkreten) Stichprobe
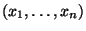 genannt.
genannt.
- Beispiel
- Während eines bestimmten Zeitraumes verkauften die 8 Angestellten
der Abteilung ,,Lebensversicherungen'' eines
Versicherungsunternehmens jeweils die folgenden Anzahlen von
Lebensversicherungsverträgen: 9, 12, 5, 13, 7, 11, 24, 11.
- Wir fassen diese Daten als Stichprobenwerte
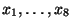 einer
Stichprobe vom Umfang
einer
Stichprobe vom Umfang 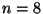 auf.
auf.
- Das Stichprobenmittel
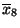 dieser Stichprobe beträgt
d.h., im Mittel wurden von den Angestellten jeweils 11.5 Verträge
während des betrachteten Zeitraumes verkauft.
dieser Stichprobe beträgt
d.h., im Mittel wurden von den Angestellten jeweils 11.5 Verträge
während des betrachteten Zeitraumes verkauft.
- Beachte
- In der obenbetrachteten Beispiel-Stichprobe ist die maximale
Anzahl der abgeschlossenen Verträge um mehr als 10 Verträge größer
als die zweitgrößte Anzahl.
- Streicht man den Maximalwert 24 aus dieser Stichprobe, so
verändert sich das Stichprobenmittel
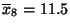 zu
zu
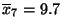 .
.
- Das Stichprobenmittel reagiert also offensichtlich ,,empfindlich''
auf extreme Werte, sogenannte Ausreißer, in den Daten.
- Weitere Eigenschaften des Stichprobenmittels
- Es gilt stets
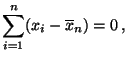 |
(3) |
d.h., das Stichprobenmittel
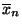 lässt sich als Schwerpunkt der Daten
lässt sich als Schwerpunkt der Daten
 interpretieren.
interpretieren.
- Außerdem kann man zeigen, dass das Stichprobenmittel
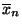 die Summe der quadratischen Abweichungen
minimiert, d.h., es gilt
die Summe der quadratischen Abweichungen
minimiert, d.h., es gilt
- Stichprobenmedian
- Lagemaßzahlen, die den Einfluss von Extremwerten begrenzen, heißen
resistent oder robust. Eine derartige robuste
Lagemaßzahl ist der Stichprobenmedian.
- Hierfür ordnet man die Stichprobenwerte
 der Größe
nach. Dies ergibt die geordnete Stichprobe
der Größe
nach. Dies ergibt die geordnete Stichprobe
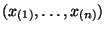 mit
mit
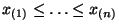 .
.
- Insbesondere gilt
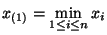 und und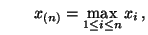 |
(4) |
d.h., 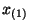 bzw.
bzw. 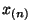 sind das Minimum bzw. das
Maximum der Stichprobenwerte
sind das Minimum bzw. das
Maximum der Stichprobenwerte
 , die auch mit
, die auch mit
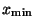 bzw.
bzw. 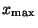 bezeichnet werden.
bezeichnet werden.
- In diesem Zusammenhang wird auch die Stichprobenspannweite
 betrachtet, die jedoch eine
Maßzahl für die Streuung der Daten ist; vgl.
Abschnitt 2.2.2.
betrachtet, die jedoch eine
Maßzahl für die Streuung der Daten ist; vgl.
Abschnitt 2.2.2.
- Manchmal ist es zweckmäßiger, anstelle des Stichprobenmittels
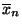 den Stichprobenmedian
den Stichprobenmedian
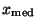 zu
betrachten, wobei
zu
betrachten, wobei
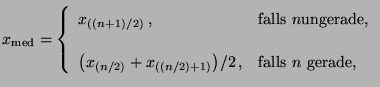 |
(5) |
- Beachte
- Der Stichprobenmedian ist also ebenfalls ein Mittelwert:
Jeweils die Hälfte der Stichprobenwerte
 ist
kleiner bzw. größer als der Stichprobenmedian
ist
kleiner bzw. größer als der Stichprobenmedian
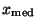 .
.
- Ein Vorteil des Stichprobenmedians
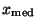 besteht darin,
dass
besteht darin,
dass
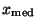 wesentlich weniger als
wesentlich weniger als
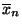 von den
extremalen Stichprobenwerten
von den
extremalen Stichprobenwerten 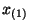 und
und 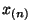 abhängt.
abhängt.
- Für das obenbetrachtete Zahlenbeispiel der Anzahlen von jeweils
verkauften Lebensversicherungsverträgen gilt
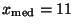 ,
und zwar sowohl für die gesamte Stichprobe aller
,
und zwar sowohl für die gesamte Stichprobe aller 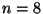 Stichprobenwerte als auch für die Teilstichprobe von
Stichprobenwerte als auch für die Teilstichprobe von 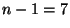 Stichprobenwerten, für die der ,,Ausreißerwert'' 24 gestrichen
wurde.
Stichprobenwerten, für die der ,,Ausreißerwert'' 24 gestrichen
wurde.
- Eine weitere allgemeine Eigenschaft des Medians
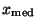 ist
die Minimierung der Summe der absoluten Abweichungen
minimiert, d.h., es gilt
ist
die Minimierung der Summe der absoluten Abweichungen
minimiert, d.h., es gilt
- Empirische Quantile
- Modus
- Derjenige Wert der Stichprobenwerte
 , der am
häufigsten auftritt, wird Modus der Stichprobe genannt und
mit
, der am
häufigsten auftritt, wird Modus der Stichprobe genannt und
mit
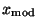 bezeichnet.
bezeichnet.
- Beachte
- Der Modus
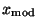 ist die wichtigste Lagemaßzahl für
nominalskalierte Merkmale.
ist die wichtigste Lagemaßzahl für
nominalskalierte Merkmale.
- Für das obenbetrachtete Zahlenbeispiel ist der Modus
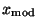 gleich 11.
gleich 11.
- Für intervallskalierte Merkmale können das Stichprobenmittel
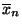 , der Median
, der Median
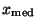 und der Modus
und der Modus
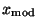 auch zur Beschreibung der Symmetrie bzw. Schiefe
der Stichprobe benutzt werden. Man spricht von einer
auch zur Beschreibung der Symmetrie bzw. Schiefe
der Stichprobe benutzt werden. Man spricht von einer
- symmetrischen Verteilung der Stichprobenwerte, falls
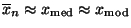 ,
,
- linkssteilen Verteilung der Stichprobenwerte, falls
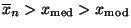 ,
,
- rechtssteilen Verteilung der Stichprobenwerte, falls
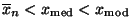 .
.
- Geometrisches und harmonisches Mittel
- Neben dem eigentlichen (arithmetischen) Stichprobenmittel und dem
Median werden in der Literatur noch weitere Ansätze zur Mittelung
der Stichprobenwerte
 betrachtet:
betrachtet:
- Das geometrische Mittel der Stichprobenwerte
 ist gegeben durch
ist gegeben durch
- und das harmonische Mittel von
 ist gegeben
durch
ist gegeben
durch
- Beispiele
- i)
- Das geometrische Mittel
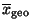 wird im
Zusammenhang mit Wachstumsfaktoren von Beständen betrachtet
(beispielsweise in der Finanz- und Versicherungswirtschaft, aber
auch bei biologischen Wachstumsmodellen):
wird im
Zusammenhang mit Wachstumsfaktoren von Beständen betrachtet
(beispielsweise in der Finanz- und Versicherungswirtschaft, aber
auch bei biologischen Wachstumsmodellen):
- ii)
- Das harmonische Mittel
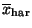 wird
beispielsweise bei der Berechnung von mittleren
Geschwindigkeiten verwendet.
wird
beispielsweise bei der Berechnung von mittleren
Geschwindigkeiten verwendet.




Next: Maßzahlen für die Streuung
Up: Kenngrößen zur Beschreibung von
Previous: Kenngrößen zur Beschreibung von
Contents
Hendrik Schmidt
2003-07-21
![]() , sogenannte Maßzahlen, die die Lage der Daten beschreiben und die kurz Lagemaßzahlen genannt werden.
, sogenannte Maßzahlen, die die Lage der Daten beschreiben und die kurz Lagemaßzahlen genannt werden.

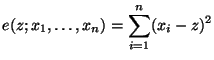
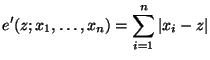
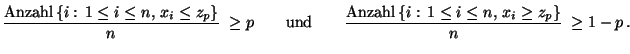
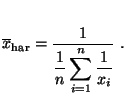
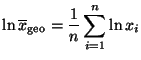 und somit
und somit