



Next: Konzentrationsmaße
Up: Kenngrößen zur Beschreibung von
Previous: Lagemaßzahlen
Contents
Maßzahlen für die Streuung der Daten
Wir betrachten nun Kenngrößen der Stichprobe
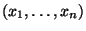 ,
die die Streuung der Daten
,
die die Streuung der Daten
 beschreiben.
beschreiben.
- Stichprobenvarianz und Stichproben-Standardabweichung
- Empirischer Variationskoeffizient
- Für die Stichprobe
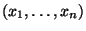 mit dem
Stichprobenmittelwert
mit dem
Stichprobenmittelwert
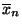 und der
Stichproben-Standardabweichung
und der
Stichproben-Standardabweichung 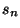 wird der empirische
Variationskoeffizient durch den Quotienten
wird der empirische
Variationskoeffizient durch den Quotienten
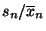 definiert.
definiert.
- Der Quotient
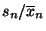 wird manchmal auch Variabilitätskoeffizient genannt.
wird manchmal auch Variabilitätskoeffizient genannt.
- Empirischer Quantilabstand
- In Verallgemeinerung der bereits erwähnten Stichprobenspannweite
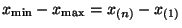 wird manchmal auch für
beliebiges
wird manchmal auch für
beliebiges
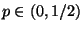 der empirische Quantilabstand
der empirische Quantilabstand
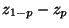 betrachtet, der ebenfalls eine Kenngröße zur
Beschreibung der Streuung der Daten
betrachtet, der ebenfalls eine Kenngröße zur
Beschreibung der Streuung der Daten
 ist.
ist.
- Insbesondere wird häufig der sogenannte Interquartilsabstand
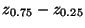 betrachtet.
betrachtet.
- Beachte




Next: Konzentrationsmaße
Up: Kenngrößen zur Beschreibung von
Previous: Lagemaßzahlen
Contents
Hendrik Schmidt
2003-07-21
![]() ,
die die Streuung der Daten
,
die die Streuung der Daten
![]() beschreiben.
beschreiben.
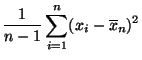
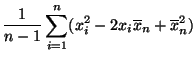
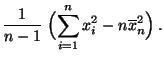
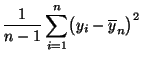
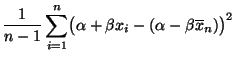
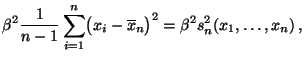
![\includegraphics[width=10cm]{wista_boxplot.eps}](img136.png)