



Next: Zusammenhangsmaße
Up: Kenngrößen zur Beschreibung von
Previous: Kontingenztafel der absoluten Häufigkeiten
Contents
Kontingenztafeln für relative bzw. bedingte Häufigkeiten
- Wenn anstelle der absoluten Häufigkeiten
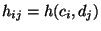 die
relativen Häufigkeiten
die
relativen Häufigkeiten
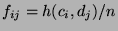 betrachtet
werden, dann ergibt sich die folgende
betrachtet
werden, dann ergibt sich die folgende
 -Kontingenztafel der relativen Häufigkeiten der Kombinationen der
Ausprägungen/Werte
-Kontingenztafel der relativen Häufigkeiten der Kombinationen der
Ausprägungen/Werte 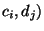 von
von 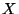 bzw.
bzw. 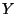 :
:
- Dabei sind
bzw.
die relativen Randhäufigkeiten der Ausprägungen/Werte von
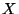 bzw.
bzw. 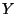 .
.
- Bei der Untersuchung der Frage, ob Zusammenhänge zwischen
den Ausprägungen/Werten von
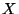 bzw.
bzw. 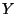 bestehen, interessieren
darüber hinaus noch die bedingten relativen Häufigkeiten
bestehen, interessieren
darüber hinaus noch die bedingten relativen Häufigkeiten
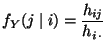 bzw. bzw.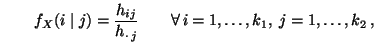 |
(14) |
wobei
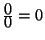 gesetzt wird.
gesetzt wird.
- Dabei sind
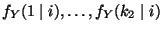 die relativen
Häufigkeiten derjenigen Ausprägungen/Werte von
die relativen
Häufigkeiten derjenigen Ausprägungen/Werte von 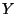 , die zusammen
mit der (fest vorgegebenen) Ausprägung
, die zusammen
mit der (fest vorgegebenen) Ausprägung 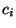 von
von 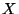 auftreten.
auftreten.
- Man spricht deshalb auch von den bedingten relativen Häufigkeiten
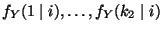 der Ausprägungen/Werte von
der Ausprägungen/Werte von
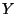 unter der Bedingung, dass
unter der Bedingung, dass 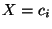 .
.
- Umgekehrt heißen
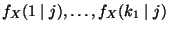 die
bedingten relativen Häufigkeiten der Ausprägungen/Werte von
die
bedingten relativen Häufigkeiten der Ausprägungen/Werte von 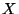 unter der Bedingung, dass
unter der Bedingung, dass 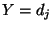 .
.
- Für das in Abschnitt 2.3.1 betrachtete Beispiel, bei
dem die Merkmale ,,Ausbildungsniveau'' und ,,Dauer der
Arbeitslosigkeit'' betrachtet wurden, ergibt sich dann die
folgende
 -Kontingenztafel der bedingten
relativen Häufigkeiten:
-Kontingenztafel der bedingten
relativen Häufigkeiten:
| |
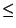 6 Monate 6 Monate |
7-12 Monate |
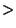 12 Monate 12 Monate |
|
| keine Ausbildung |
0.699 |
0.154 |
0.147 |
1 |
| Lehre |
0.730 |
0.184 |
0.086 |
1 |
| fachspez. Ausbildung |
0.714 |
0.197 |
0.089 |
1 |
| Hochschulabschluss |
0.800 |
0.114 |
0.086 |
1 |




Next: Zusammenhangsmaße
Up: Kenngrößen zur Beschreibung von
Previous: Kontingenztafel der absoluten Häufigkeiten
Contents
Hendrik Schmidt
2003-07-21