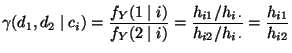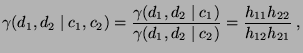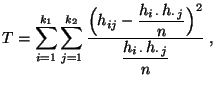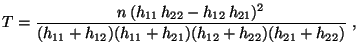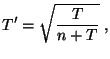- Wir betrachten zunächst den Spezialfall
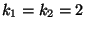 , d.h., die
Merkmale/Kenngrößen/Variablen
, d.h., die
Merkmale/Kenngrößen/Variablen 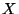 und
und 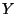 besitzen jeweils nur
zwei verschiedene Ausprägungen/Werte.
besitzen jeweils nur
zwei verschiedene Ausprägungen/Werte.
- Die entsprechende
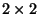 -Kontingenztafel hat somit die Form
-Kontingenztafel hat somit die Form
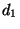
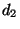
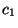
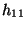
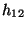
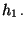
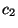
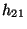
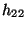
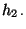
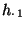
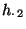
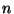
- Für jedes
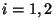 heißt der Quotient der bedingten relativen
Häufigkeiten
heißt der Quotient der bedingten relativen
Häufigkeiten
die bedingte Chance für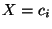 , wobei
, wobei 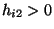 vorausgesetzt wird.
vorausgesetzt wird.
- Hieraus ergibt sich ein einfaches Zusammenhangsmaß zwischen den
Chancen der ersten bzw. zweiten Zeile der
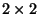 -Kontingenztafel, das relative Chance genannt wird und
gegeben ist durch den Quotienten
-Kontingenztafel, das relative Chance genannt wird und
gegeben ist durch den Quotienten
wobei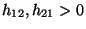 vorausgesetzt wird.
vorausgesetzt wird.
- Beispiel
- Für das in Abschnitt 2.3.1 diskutierte Beispiel
betrachten wir jetzt nur die Ausprägungen ,,fachspezifische
Ausbildung'' (F) bzw. ,,Hochschulabschluss'' (H) für das Merkmal
,,Ausbildungsniveau'' sowie die Ausprägungen
,,Kurzzeitarbeitslosigkeit'' (
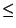 6 Monate) bzw. ,,mittel- und
langfristige Arbeitslosigkeit'' (
6 Monate) bzw. ,,mittel- und
langfristige Arbeitslosigkeit'' (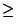 7 Monate) für das Merkmal
,,Dauer der Arbeitslosigkeit''.
7 Monate) für das Merkmal
,,Dauer der Arbeitslosigkeit''.
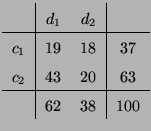
- Dann ergibt sich die folgende
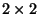 -Kontingenztafel
der absoluten Häufigkeiten:
-Kontingenztafel
der absoluten Häufigkeiten:
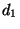
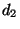
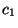
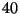
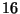
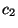
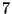
- Die ,,bedingte Chance''
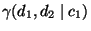 von Personen mit
fachspezifischer Ausbildung, kurzfristig arbeitslos zu sein
(gegenüber einer mittel- bzw. langfristigen Arbeitslosigkeit), ist
also gegeben durch
von Personen mit
fachspezifischer Ausbildung, kurzfristig arbeitslos zu sein
(gegenüber einer mittel- bzw. langfristigen Arbeitslosigkeit), ist
also gegeben durch
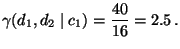
- Für Personen mit Hochschulabschluss ergibt sich dagegen der Wert
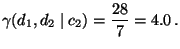
- Für die ,,relative Chance'' ergibt sich
d.h., für Personen mit Hochschulabschluss stehen somit die ,,Chancen'' deutlich besser.
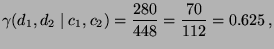
- Für das in Abschnitt 2.3.1 diskutierte Beispiel
betrachten wir jetzt nur die Ausprägungen ,,fachspezifische
Ausbildung'' (F) bzw. ,,Hochschulabschluss'' (H) für das Merkmal
,,Ausbildungsniveau'' sowie die Ausprägungen
,,Kurzzeitarbeitslosigkeit'' (
- Beachte
- Die Begriffe der bedingten bzw. relativen Chance lassen sich völlig analog auch für den Fall definieren, dass Merkmale mit mehr als 2 Ausprägungen betrachtet werden.
- Die relative Chance zwischen
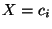 und
und
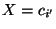 bezüglich der bedingten Chancen von
bezüglich der bedingten Chancen von 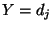 und
und
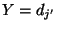 ist dann gegeben durch
ist dann gegeben durch
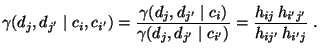
- Wir definieren nun den
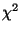 -Koeffizienten der beiden
Stichproben
-Koeffizienten der beiden
Stichproben
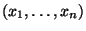 und
und
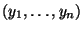 ,
,
- der eine weitere Maßzahl zur Beschreibung des (eventuell
vorhandenen) Zusammenhanges zwischen den Werten der Stichproben
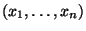 und
und
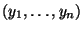 der beiden Markmale
der beiden Markmale 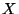 und
und 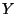 ist,
ist,
- wobei wir das Nichtvorhandensein eines solchen Zusammenhanges mit
Hilfe der bedingten relativen Häufigkeiten
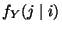 beschreiben, die in (14) eingeführt worden sind.
beschreiben, die in (14) eingeführt worden sind.
- der eine weitere Maßzahl zur Beschreibung des (eventuell
vorhandenen) Zusammenhanges zwischen den Werten der Stichproben
- Man erwartet, dass die bedingten relativen Häufigkeiten
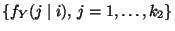 in diesem Fall
in diesem Fall
- nicht von
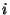 abhängen,
abhängen,
- was gleichbedeutend damit ist, dass
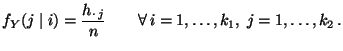
- nicht von
- Mit anderen Worten: Falls die Ausprägungen/Werte der
Merkmale/Kenngrößen/Variablen
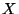 und
und 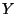 keinen Zusammmenhang
aufweisen (d.h. unabhängig sind), dann sollte die (in diesem
Fall) erwartete Häufigkeit
keinen Zusammmenhang
aufweisen (d.h. unabhängig sind), dann sollte die (in diesem
Fall) erwartete Häufigkeit
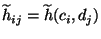 , mit der die Kombination
, mit der die Kombination 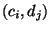 der Ausprägungen
der Ausprägungen
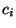 und
und 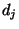 auftritt, für jedes
auftritt, für jedes
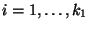 unf für jedes
unf für jedes
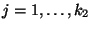
- der folgenden Gleichung genügen:
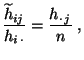
- d.h., gegeben sein durch den Produkt-Ansatz
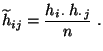
- der folgenden Gleichung genügen:
- Beachte
- Falls die Ausprägungen/Werte der Merkmale/Kenngrößen/Variablen
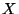 und
und 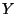 keinen Zusammenhang aufweisen, dann sollten sich die
(tatsächlich beobachteten) Häufigkeiten
keinen Zusammenhang aufweisen, dann sollten sich die
(tatsächlich beobachteten) Häufigkeiten 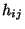 und die (zu
erwartenden) Häufigkeiten
und die (zu
erwartenden) Häufigkeiten
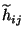 nicht zu sehr
voneinander unterscheiden.
nicht zu sehr
voneinander unterscheiden.
- Als Zusammenhangsmaß betrachtet man deshalb den
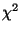 -Koeffizienten
-Koeffizienten 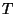 , der eine sogenannte Testgröße ist und
gegeben ist durch
, der eine sogenannte Testgröße ist und
gegeben ist durch
wobei vorausgesetzt wird, dass sämtliche Randhäufigkeiten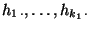 sowie
sowie
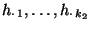 positiv sind, und die Division durch
positiv sind, und die Division durch
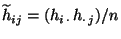 lediglich der
Normierung dient.
lediglich der
Normierung dient.
- Im Spezialfall einer
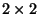 -Kontingenztafel
-Kontingenztafel
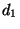
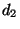
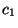
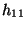
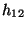
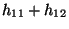
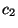
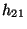
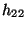
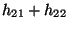
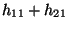
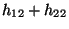
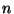
lässt sich der in (17) definierte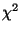 -Koeffizient
-Koeffizient 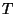 leicht berechnen, denn in diesem Fall
gilt
leicht berechnen, denn in diesem Fall
gilt
wobei vorausgesetzt wird, dass die Randhäufigkeiten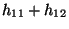 ,
,
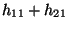 ,
,
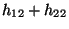 und
und
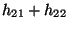 positiv sind.
positiv sind.
- Falls die Ausprägungen/Werte der Merkmale/Kenngrößen/Variablen
- Für den in (17) definierten
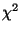 -Koeffizienten
gilt stets
-Koeffizienten
gilt stets 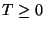 , wobei
, wobei
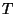 groß ist, wenn ein Zusammenhang zwischen
groß ist, wenn ein Zusammenhang zwischen 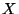 und
und 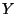 besteht,
besteht,
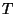 klein ist, wenn
klein ist, wenn 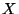 und
und 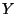 voneinander unabhängig sind.
voneinander unabhängig sind.
- Um genauer sagen zu können, wann
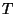 als klein bzw. groß anzusehen
ist, sind tieferliegende mathematische Modelle der beurteilenden Statistik erforderlich, insbesondere sogenannte
Signifikanztests zum Überprüfen von Modellannahmen; vgl.
beispielsweise
als klein bzw. groß anzusehen
ist, sind tieferliegende mathematische Modelle der beurteilenden Statistik erforderlich, insbesondere sogenannte
Signifikanztests zum Überprüfen von Modellannahmen; vgl.
beispielsweise
- das Skript zum Grundkurs "Stochastik für Wirtschaftswissenschaftler" unter der Internet-Adresse:
- oder die Kapitel 3 und
![[*]](file:/usr/local/lib/latex2html/icons/crossref.png) des
jetzigen Vorlesungsskriptes.
des
jetzigen Vorlesungsskriptes.
- Der in (17) definierte
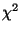 -Koeffizient
-Koeffizient 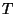 hat
den Nachteil, dass der Wertebereich von
hat
den Nachteil, dass der Wertebereich von 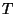 vom Umfang
vom Umfang 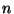 der
Stichproben
der
Stichproben
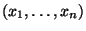 bzw.
bzw.
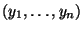 abhängt.
abhängt.
- Dieser Nachteil wird eliminiert, wenn anstelle des
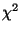 -Koeffizienten
-Koeffizienten 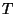 der Kontingenzkoeffizient
der Kontingenzkoeffizient
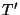 betrachtet wird,
betrachtet wird,
- der gegeben ist durch
- wobei
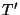 nur Werte zwischen 0 und
nur Werte zwischen 0 und
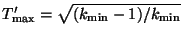 annehmen kann;
annehmen kann;
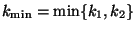 .
.
- der gegeben ist durch
- Ein gewisser Nachteil des Kontingenzkoeffizienten
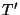 besteht noch darin, dass der Wertebereich der Testgröße
besteht noch darin, dass der Wertebereich der Testgröße 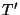 von den Anzahlen
von den Anzahlen 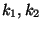 der Ausprägungen von
der Ausprägungen von 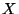 bzw.
bzw. 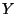 abhängt.
abhängt.
- Durch einen weiteren Normierungsschritt wird deshalb der
sogenannte korrigierte Kontingenzkoeffizient
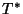 eingeführt, der gegeben ist durch
und der nur Werte im Einheitsintervall
eingeführt, der gegeben ist durch
und der nur Werte im Einheitsintervall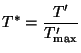
![$ [0,1]$](img7.png) annehmen kann.
annehmen kann.
- Beispiel
- Für das in Abschnitt 2.3.1 eingeführte Beispiel
betrachten wir nun die Ausprägungen ,,keine Ausbildung'' bzw.
,,Lehre'' für das Merkmal ,,Ausbildungsniveau'' sowie die
Ausprägungen ,,mittelfristige Arbeitslosigkeit'' (7-12 Monate)
bzw. ,,langfristige Arbeitslosigkeit (
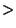 12 Monate) für das
Merkmal ,,Dauer der Arbeitslosigkeit''.
12 Monate) für das
Merkmal ,,Dauer der Arbeitslosigkeit''.
- Dann ergibt sich die folgende
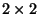 -Kontingenztafel
der absoluten Häufigkeiten:
-Kontingenztafel
der absoluten Häufigkeiten:
- Hieraus und aus (18) ergibt sich, dass
sowie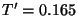 bzw.
bzw. 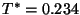 .
.
- Für das in Abschnitt 2.3.1 eingeführte Beispiel
betrachten wir nun die Ausprägungen ,,keine Ausbildung'' bzw.
,,Lehre'' für das Merkmal ,,Ausbildungsniveau'' sowie die
Ausprägungen ,,mittelfristige Arbeitslosigkeit'' (7-12 Monate)
bzw. ,,langfristige Arbeitslosigkeit (