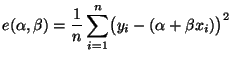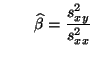- dass die Regressionsfunktion
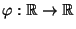 die in
(34) gegebene Form besitzt, d.h., wir betrachten
das lineare Regressionsmodell,
die in
(34) gegebene Form besitzt, d.h., wir betrachten
das lineare Regressionsmodell,
- und passen die Gerade
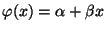 , die auch Ausgleichsgerade genannt wird, mit der Methode der kleinsten
Quadrate an die Datenpunkte
, die auch Ausgleichsgerade genannt wird, mit der Methode der kleinsten
Quadrate an die Datenpunkte
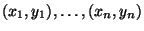 an.
an.
- wie die unbekannten Modellparameter
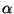 und
und 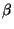 zu wählen
sind, um den mittleren quadratischen Fehler
zu wählen
sind, um den mittleren quadratischen Fehler
zu minimieren, und setzen dabei voraus, - dass
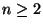 und dass nicht alle Ausprägungen
und dass nicht alle Ausprägungen
 von
von 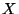 einander gleich sind.
einander gleich sind.
den mittleren quadratischen Fehler
- wobei
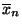 ,
,
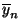 so wie bisher die
Stichprobenmittel von
so wie bisher die
Stichprobenmittel von
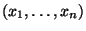 bzw.
bzw.
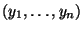 bezeichnen, d.h.
bezeichnen, d.h.
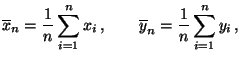
- und die Stichprobenvarianzen
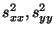 bzw. die
Stichprobenkovarianz
bzw. die
Stichprobenkovarianz 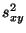 gegeben sind durch
gegeben sind durch
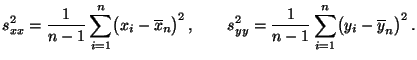
- Die in (36) angegebene Lösung
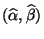 des Minimierungsproblems lässt
sich wie folgt herleiten.
des Minimierungsproblems lässt
sich wie folgt herleiten.
- Wenn man die Funktion
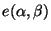 nach
nach 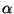 differenziert, so erkennt man, dass für jedes
differenziert, so erkennt man, dass für jedes
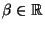 die Zahl
den Wert des folgenden Ausdruckes minimiert:
die Zahl
den Wert des folgenden Ausdruckes minimiert: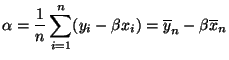
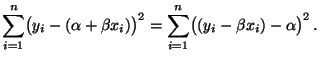
- Mit anderen Worten: Für jedes
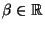 ist
ist
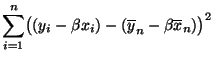
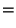
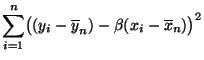
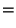
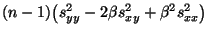
der kleinste Wert des mittleren quadratischen Fehlers. - Durch Differenzieren dieses Ausdruckes nach
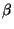 ergibt sich
nun, dass das globale Minimum an der folgenden Stelle angenommen
wird;
ergibt sich
nun, dass das globale Minimum an der folgenden Stelle angenommen
wird;
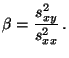
- Für das in Abschnitt 2.4.4 betrachtete Beispiel der
beiden Merkmale ,,Geburtsgewicht'' und ,,Gewichtszunahme''
ergibt sich, dass
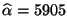 und
und
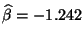 .
.
- An das Streudiagramm dieses Datensatzes lässt sich somit die
folgende Regressionsgerade anpassen:
![\includegraphics[width=8cm]{wista_linreg252_1.eps}](img479.png)
- Der in (35) definierte mittlere quadratische Fehler
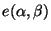 ist der mittlere quadratische vertikale
Abstand zwischen den ,,beobachteten'' Punkten
ist der mittlere quadratische vertikale
Abstand zwischen den ,,beobachteten'' Punkten 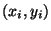 und den
entsprechenden Punkten
und den
entsprechenden Punkten
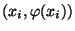 auf der
Regressionsgeraden
auf der
Regressionsgeraden
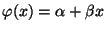 an den Stellen
an den Stellen
 .
.
- Anstelle der vertikalen Abstände kann man beispielsweise auch die
horizontalen Abstände betrachten. Durch Vertauschen der Rollen von
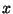 und
und 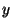 ergibt sich dann, dass
die optimalen Werte der Parameter
ergibt sich dann, dass
die optimalen Werte der Parameter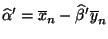 und
und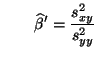
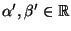 der (inversen)
Regressionsgeraden
der (inversen)
Regressionsgeraden
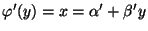 sind.
sind.
- Wenn wir diese Geradengleichung nach
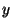 auflösen, dann ergibt
sich die Gleichung
wobei allerdings die Werte
auflösen, dann ergibt
sich die Gleichung
wobei allerdings die Werte
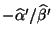 und
und
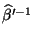 für Regressionskonstante bzw.
Regressionskoeffizient im allgemeinen verschieden von den
optimalen Werten
für Regressionskonstante bzw.
Regressionskoeffizient im allgemeinen verschieden von den
optimalen Werten
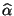 bzw.
bzw.
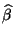 sind, die
in (36) hergeleitet worden sind.
sind, die
in (36) hergeleitet worden sind.
- Bestimmen Sie für das in Abschnitt 2.4.1 betrachtete
Beispiel der Merkmale ,,Clusterzahl je Traube'' unsd
,,Jahresertrag'' die Werte
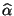 und
und
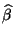 sowie
sowie
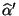 und
und
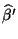 und
zeichnen Sie die beiden Regressionsgeraden in das Streudiagramm
dieses Datensatzes ein.
und
zeichnen Sie die beiden Regressionsgeraden in das Streudiagramm
dieses Datensatzes ein.
- Prognostizieren Sie mit Hilfe der Regressionsgerade
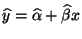 den Jahresertrag, der einer
mittleren Clusterzahl von 100 Beeren je Traube entsprechen würde.
den Jahresertrag, der einer
mittleren Clusterzahl von 100 Beeren je Traube entsprechen würde.