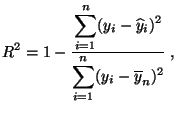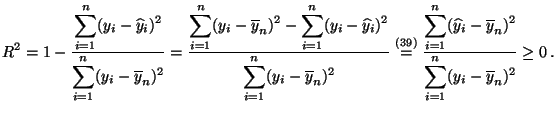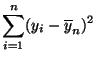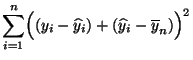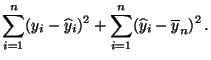- die Anpassungsgüte des Regressionsmodells
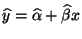 an die beobachteten Werte
an die beobachteten Werte
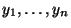 der Zielvariablen
der Zielvariablen 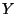 beschreibt,
beschreibt,
- falls die Regressionskonstante
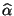 und der
Regressionskoeffizient
und der
Regressionskoeffizient
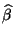 durch (36)
gegeben sind.
durch (36)
gegeben sind.
- für jedes
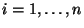 die Abweichung
die Abweichung
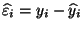 des
beobachteten Wertes
des
beobachteten Wertes 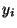 von dem entsprechenden Wert
von dem entsprechenden Wert
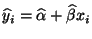 der Regressionsfunktion
der Regressionsfunktion
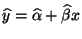 ,
,
- wobei die Abweichungen
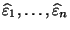 auch
Residuen genannt werden und
auch
Residuen genannt werden und
- der in (35) eingeführte mittlere quadratische
Fehler
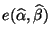 das arithmetische Mittel
der Abweichungsquadrate
das arithmetische Mittel
der Abweichungsquadrate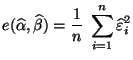
 ist.
ist.
- je größer die sogenannte Residualstreuung
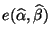 ist,
ist,
- wobei diese (absolute) Abweichungsmaßzahl noch mit der Gesamtstreuung
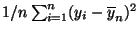 der
beobachteten Werte
der
beobachteten Werte
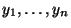 normiert wird.
normiert wird.
die auch Determinationskoeffizient genannt wird.
- Das Bestimmtheitsmaß
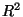 nimmt nur Werte zwischen 0 und
nimmt nur Werte zwischen 0 und 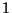 an, d.h., es gilt stets
an, d.h., es gilt stets
- Außerdem gilt
- d.h., das Bestimmtheitsmaß
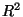 stimmt mit dem Quadrat des
empirischen Korrelationskoeffizienten
stimmt mit dem Quadrat des
empirischen Korrelationskoeffizienten 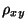 überein, der in
Abschnitt 2.4.2 eingeführt wurde, wobei sich die
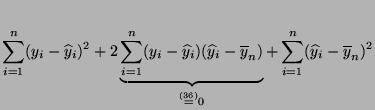
Gültigkeit von (40) aus den folgenden Überlegungen
ergibt.
überein, der in
Abschnitt 2.4.2 eingeführt wurde, wobei sich die
Gültigkeit von (40) aus den folgenden Überlegungen
ergibt.
- Aus (36) folgt zunächst, dass das arithmetische
Mittel
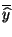 von
von
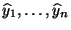 mit dem Stichprobenmittel
mit dem Stichprobenmittel
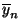 übereinstimmt, denn
es gilt
übereinstimmt, denn
es gilt
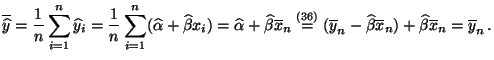
- Hieraus ergibt sich, dass
und somit
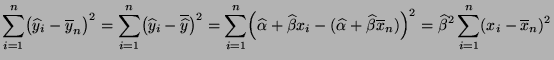
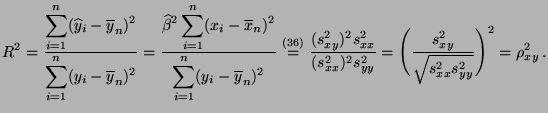
- d.h., das Bestimmtheitsmaß